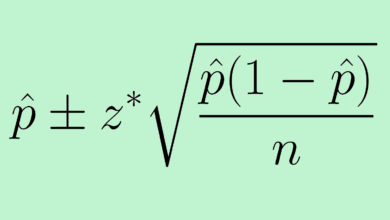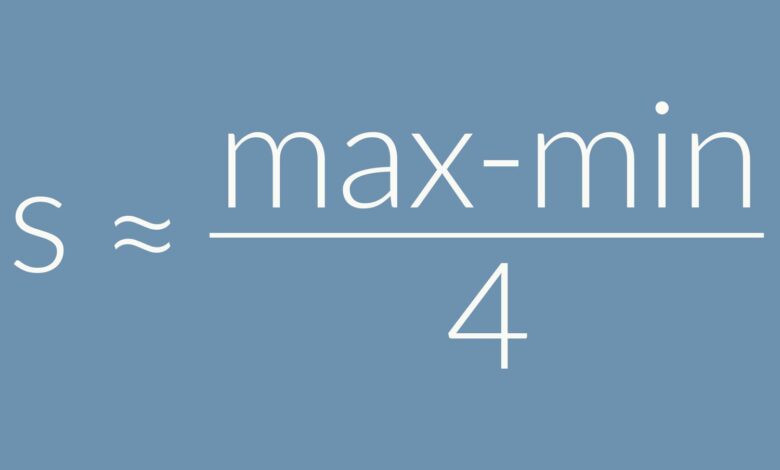
Contents
L’écart-type et l’étendue sont deux mesures de la diffusion d’un ensemble de données. Chaque nombre nous indique à sa manière l’écart des données, car ils sont tous deux une mesure de la variation. Bien qu’il n’y ait pas de relation explicite entre la fourchette et l’écart type, il existe une règle empirique qui peut être utile pour relier ces deux statistiques. Cette relation est parfois appelée règle de l’intervalle pour l’écart-type.
La règle de l’intervalle nous dit que l’écart-type d’un échantillon est approximativement égal à un quart de l’intervalle des données. En d’autres termes, l’écart type d’un échantillon est s = (Maximum – Minimum)/4. Il s’agit d’une formule très simple à utiliser, qui ne doit être utilisée que comme une estimation très approximative de l’écart-type.
Un exemple
Pour voir un exemple du fonctionnement de la règle de la fourchette, nous allons nous pencher sur l’exemple suivant. Supposons que nous commencions avec les valeurs de données de 12, 12, 14, 15, 16, 18, 18, 20, 20, 25. Ces valeurs ont une moyenne de 17 et un écart-type d’environ 4,1. Si, au contraire, nous calculons d’abord la plage de nos données comme étant 25 – 12 = 13 et que nous divisons ensuite ce nombre par quatre, nous obtenons notre estimation de l’écart type comme étant 13/4 = 3,25. Ce chiffre est relativement proche de l’écart-type réel et est bon pour une estimation approximative.
Pourquoi cela fonctionne-t-il ?
Il peut sembler que la règle de la portée soit un peu étrange. Pourquoi fonctionne-t-elle ? Ne semble-t-il pas complètement arbitraire de diviser simplement la portée par quatre ? Pourquoi ne diviserions-nous pas par un nombre différent ? Il y a en fait une justification mathématique qui se passe en coulisses.
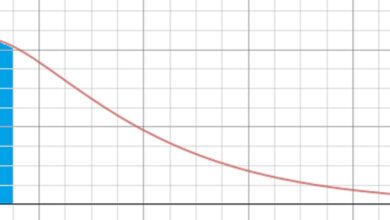
Rappelez-vous les propriétés de la courbe en cloche et les probabilités d’une distribution normale standard. Une des caractéristiques concerne la quantité de données qui se situe dans un certain nombre d’écarts types :
- Environ 68 % des données se situent à un écart type près (supérieur ou inférieur) de la moyenne.
- Environ 95 % des données se situent à deux écarts types près (plus ou moins élevés) de la moyenne.
- Environ 99 % se situent à trois écarts types près (supérieurs ou inférieurs) de la moyenne.
Le chiffre que nous utiliserons concerne 95%. Nous pouvons dire que 95 % de deux écarts types en dessous de la moyenne à deux écarts types au-dessus de la moyenne, nous avons 95 % de nos données. Ainsi, la quasi-totalité de notre distribution normale s’étendrait sur un segment de ligne d’une longueur totale de quatre écarts types.
Toutes les données ne sont pas normalement distribuées et en forme de courbe en cloche. Mais la plupart des données sont suffisamment bien gérées pour que deux écarts-types par rapport à la moyenne capturent presque toutes les données. Nous estimons et disons que quatre écarts types correspondent approximativement à la taille de la plage, et donc que la plage divisée par quatre est une approximation de l’écart type.
Utilisations de la règle de la fourchette
La règle de la fourchette est utile dans un certain nombre de cas. Tout d’abord, il s’agit d’une estimation très rapide de l’écart type. L’écart-type exige que nous trouvions d’abord la moyenne, puis que nous soustrayions cette moyenne de chaque point de données, que nous mettions au carré les différences, que nous les ajoutions, que nous divisions par un de moins que le nombre de points de données, puis que nous prenions (finalement) la racine carrée. D’autre part, la règle de l’intervalle ne nécessite qu’une soustraction et une division.
La règle de la fourchette est également utile lorsque les informations dont nous disposons sont incomplètes. Des formules telles que celle qui permet de déterminer la taille de l’échantillon nécessitent trois informations : la marge d’erreur souhaitée, le niveau de confiance et l’écart type de la population que nous étudions. Souvent, il est impossible de connaître l’écart type de la population. Avec la règle de l’intervalle, nous pouvons estimer cette statistique, puis savoir quelle taille doit avoir notre échantillon.