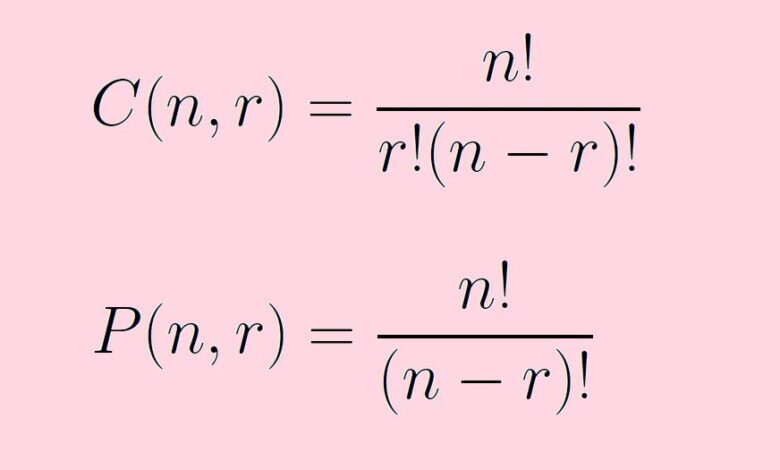
Contents
Tout au long des mathématiques et des statistiques, nous devons savoir compter. Cela est particulièrement vrai pour certains problèmes de probabilité. Supposons que l’on nous donne un total de n objets distincts et que nous voulions sélectionner r d’entre eux. Cela touche directement à un domaine des mathématiques connu sous le nom de combinatoire, qui est l’étude du comptage. Deux des principales façons de compter ces r objets à partir de n éléments sont appelées permutations et combinaisons. Ces concepts sont étroitement liés les uns aux autres et se confondent facilement.
Quelle est la différence entre une combinaison et une permutation ? L’idée clé est celle de l’ordre. Une permutation fait attention à l’ordre dans lequel nous sélectionnons nos objets. Le même ensemble d’objets, mais pris dans un ordre différent, nous donnera des permutations différentes. Avec une combinaison, nous sélectionnons toujours r objets sur un total de n, mais l’ordre n’est plus pris en compte.
Un exemple de permutations
Pour distinguer ces idées, nous allons considérer l’exemple suivant : combien y a-t-il de permutations de deux lettres de l’ensemble {a,b,c} ?
Ici, nous énumérons toutes les paires d’éléments de l’ensemble donné, tout en faisant attention à l’ordre. Il y a un total de six permutations. La liste de tous ces éléments est la suivante : ab, ba, bc, cb, ac et ca. Notez que les permutations ab et ba sont différentes car dans un cas, a a été choisi en premier et dans l’autre, a a été choisi en second.
Un exemple de combinaisons
Nous allons maintenant répondre à la question suivante : combien y a-t-il de combinaisons de deux lettres de l’ensemble {a,b,c} ?
Comme il s’agit de combinaisons, nous ne nous soucions plus de l’ordre. Nous pouvons résoudre ce problème en examinant les permutations et en éliminant celles qui comportent les mêmes lettres. En tant que combinaisons, ab et ba sont considérés comme identiques. Il n’y a donc que trois combinaisons : ab, ac et bc.
Formules
Dans les situations où nous rencontrons des ensembles plus importants, il est trop long de dresser la liste de toutes les permutations ou combinaisons possibles et de compter le résultat final. Heureusement, il existe des formules qui nous donnent le nombre de permutations ou de combinaisons de n objets prises r à la fois.
Dans ces formules, nous utilisons la notation abrégée de n ! appelée n factoriel. La factorielle dit simplement de multiplier ensemble tous les nombres entiers positifs inférieurs ou égaux à n. Ainsi, par exemple, 4 ! = 4 x 3 x 2 x 1 = 24. Par définition, 0 ! = 1.
Le nombre de permutations de n objets prises r à la fois est donné par la formule :
P(n,r) = n!/(n – r) !
Le nombre de combinaisons de n objets pris r à la fois est donné par la formule :
C(n,r) = n!/[r!(n – r)!]
Les formules au travail
Pour voir les formules à l’œuvre, examinons l’exemple initial. Le nombre de permutations d’un ensemble de trois objets pris deux à la fois est donné par P(3,2) = 3!/(3 – 2) ! = 6/1 = 6. Cela correspond exactement à ce que nous avons obtenu en énumérant toutes les permutations.
Le nombre de combinaisons d’un ensemble de trois objets pris deux à la fois est donné par
C(3,2) = 3!/[2!(3-2)!] = 6/2 = 3. Encore une fois, cela correspond exactement à ce que nous avons vu auparavant.
Les formules permettent de gagner du temps lorsqu’on nous demande de trouver le nombre de permutations d’un ensemble plus important. Par exemple, combien y a-t-il de permutations d’un ensemble de dix objets pris trois à la fois ? Il faudrait un certain temps pour énumérer toutes les permutations, mais avec les formules, nous voyons qu’il y en aurait :
P(10,3) = 10!/(10-3) ! = 10!/7 ! = 10 x 9 x 8 = 720 permutations.
L’idée principale
Quelle est la différence entre les permutations et les combinaisons ? L’essentiel est que dans les situations de comptage qui impliquent un ordre, il faut utiliser des permutations. Si l’ordre n’est pas important, il faut alors utiliser des combinaisons.