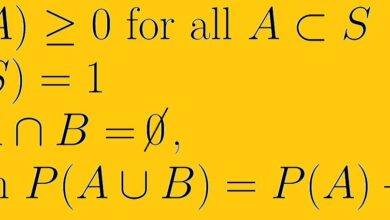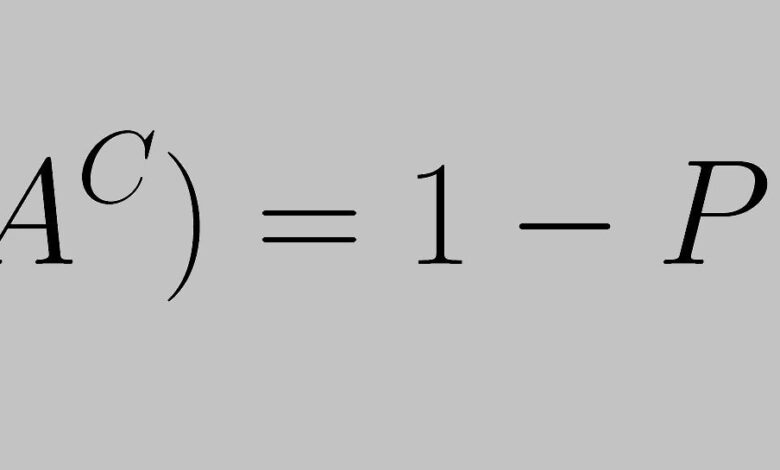
Contents
Plusieurs théorèmes de probabilité peuvent être déduits des axiomes de la probabilité. Ces théorèmes peuvent être appliqués pour calculer les probabilités que nous pouvons souhaiter connaître. L’un de ces résultats est connu sous le nom de règle du complément. Cette règle nous permet de calculer la probabilité d’un événement A en connaissant la probabilité du complément AC. Après avoir énoncé la règle du complément, nous verrons comment ce résultat peut être prouvé.
La règle du complément
Le complément de l’événement A est désigné par AC. Le complément de A est l’ensemble de tous les éléments de l’ensemble universel, ou espace échantillon S, qui ne sont pas des éléments de l’ensemble A.
La règle du complément est exprimée par l’équation suivante :
P(AC) = 1 – P(A)
On voit ici que la probabilité d’un événement et la probabilité de son complément doivent s’additionner à 1.
Preuve de la règle du complément
Pour prouver la règle du complément, nous commençons par les axiomes de la probabilité. Ces énoncés sont supposés sans preuve. Nous verrons qu’ils peuvent être systématiquement utilisés pour prouver notre affirmation concernant la probabilité du complément d’un événement.
- Le premier axiome de la probabilité est que la probabilité de tout événement est un nombre réel non négatif.
- Le deuxième axiome de la probabilité est que la probabilité de l’ensemble de l’espace d’échantillonnage S est un. Symboliquement, on écrit P(S) = 1.
- Le troisième axiome de la probabilité stipule que si A et B s’excluent mutuellement (c’est-à-dire qu’ils ont une intersection vide), alors nous indiquons la probabilité de l’union de ces événements comme suit : P(A U B ) = P(A) + P(B).
Pour la règle du complément, nous n’aurons pas besoin d’utiliser le premier axiome de la liste ci-dessus.
Pour prouver notre affirmation, nous considérons les événements Aet AC. D’après la théorie des ensembles, nous savons que ces deux ensembles ont une intersection vide. Cela est dû au fait qu’un élément ne peut pas être simultanément dans A et non dans A. Comme il y a une intersection vide, ces deux ensembles sont mutuellement exclusifs.
L’union des deux événements A et AC est également importante. Il s’agit d’événements exhaustifs, ce qui signifie que l’union de ces événements est l’ensemble de l’espace échantillon S.
Ces faits, combinés avec les axiomes, nous donnent l’équation
1 = P(S) = P(A U AC) = P(A) + P(AC) .
La première égalité est due au deuxième axiome de probabilité. La deuxième égalité est due au fait que les événements A et AC sont exhaustifs. La troisième égalité est due au troisième axiome de probabilité.
L’équation ci-dessus peut être réorganisée sous la forme que nous avons indiquée plus haut. Tout ce que nous devons faire est de soustraire la probabilité de A des deux côtés de l’équation. Ainsi,
1 = P(A) + P(AC)
devient l’équation
P(AC) = 1 – P(A).
Bien sûr, nous pourrions aussi exprimer la règle en disant cela :
P(A) = 1 – P(AC).
Ces trois équations sont des manières équivalentes de dire la même chose. Nous voyons par cette preuve comment deux axiomes et une théorie des ensembles nous aident beaucoup à prouver de nouvelles affirmations concernant la probabilité.