Contents
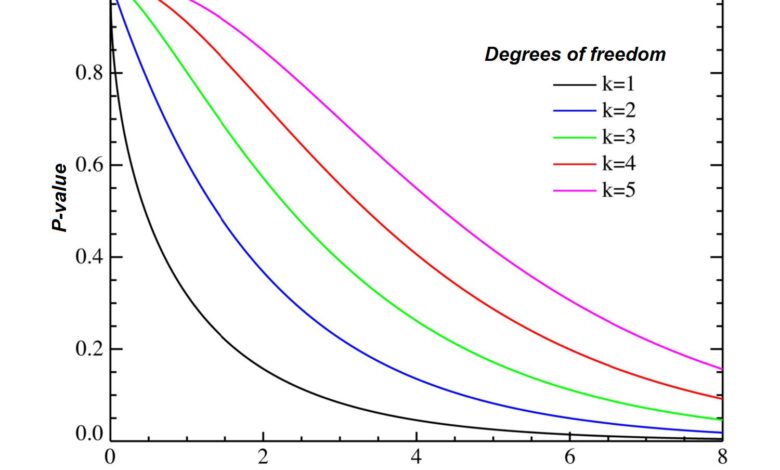
De nombreux problèmes d’inférence statistique nous obligent à trouver le nombre de degrés de liberté. Le nombre de degrés de liberté sélectionne une distribution de probabilité unique parmi un nombre infini de degrés de liberté. Cette étape est un détail souvent négligé mais crucial tant pour le calcul des intervalles de confiance que pour le fonctionnement des tests d’hypothèses.
Il n’existe pas de formule générale unique pour le nombre de degrés de liberté. Cependant, il existe des formules spécifiques utilisées pour chaque type de procédure dans les statistiques inférentielles. En d’autres termes, le cadre dans lequel nous travaillons déterminera le nombre de degrés de liberté. Ce qui suit est une liste partielle de certaines des procédures d’inférence les plus courantes, ainsi que le nombre de degrés de liberté qui sont utilisés dans chaque situation.
Distribution normale standard
Les procédures impliquant une distribution normale standard sont énumérées par souci d’exhaustivité et pour dissiper certaines idées fausses. Ces procédures n’exigent pas que nous trouvions le nombre de degrés de liberté. La raison en est qu’il existe une seule distribution normale standard. Ces types de procédures englobent celles qui impliquent une moyenne de population lorsque l’écart type de la population est déjà connu, ainsi que les procédures concernant les proportions de la population.
Un exemple de procédures T
Parfois, la pratique statistique nous oblige à utiliser la distribution en t de Student. Pour ces procédures, comme celles qui portent sur une moyenne de population dont l’écart-type est inconnu, le nombre de degrés de liberté est inférieur de un à la taille de l’échantillon. Ainsi, si la taille de l’échantillon est n, alors il y a n – 1 degrés de liberté.
Procédures T avec données appariées
Il est souvent judicieux de traiter les données comme des paires. L’appariement est généralement effectué en raison d’un lien entre la première et la deuxième valeur de notre paire. Souvent, nous apparions les données avant et après les mesures. Notre échantillon de données couplées n’est pas indépendant ; cependant, la différence entre chaque paire est indépendante. Ainsi, si l’échantillon comporte un total de n paires de points de données (pour un total de 2n valeurs), alors il y a n – 1 degrés de liberté.
T Procédures pour deux populations indépendantes
Pour ce type de problèmes, nous utilisons toujours une distribution en t. Cette fois, il y a un échantillon de chacune de nos populations. Bien qu’il soit préférable que ces deux échantillons soient de la même taille, cela n’est pas nécessaire pour nos procédures statistiques. Nous pouvons donc avoir deux échantillons de taille n1 et n2. Il y a deux façons de déterminer le nombre de degrés de liberté. La méthode la plus précise est d’utiliser la formule de Welch, une formule compliquée sur le plan du calcul, qui implique les tailles des échantillons et les écarts types des échantillons. Une autre approche, appelée approximation prudente, peut être utilisée pour estimer rapidement les degrés de liberté. Il s’agit simplement du plus petit des deux nombres n1 – 1 et n2 – 1.
Le Chi carré pour l’indépendance
L’une des utilisations du test du chi carré est de voir si deux variables catégorielles, chacune à plusieurs niveaux, présentent une indépendance. Les informations relatives à ces variables sont enregistrées dans un tableau à double sens comportant r lignes et c colonnes. Le nombre de degrés de liberté est le produit (r – 1)(c – 1).
Le chi carré de la bonne forme physique
Le chi carré de la qualité de l’ajustement commence par une seule variable catégorielle avec un total de n niveaux. Nous testons l’hypothèse selon laquelle cette variable correspond à un modèle prédéterminé. Le nombre de degrés de liberté est inférieur de un au nombre de niveaux. En d’autres termes, il y a n – 1 degrés de liberté.
ANOVA à un facteur
L’analyse factorielle de la variance (ANOVA) nous permet d’effectuer des comparaisons entre plusieurs groupes, éliminant ainsi la nécessité d’effectuer plusieurs tests d’hypothèses par paires. Comme le test nous oblige à mesurer à la fois la variation entre plusieurs groupes et la variation au sein de chaque groupe, nous obtenons deux degrés de liberté. La statistique F, qui est utilisée pour l’ANOVA d’un facteur, est une fraction. Le numérateur et le dénominateur ont chacun des degrés de liberté. Soit c le nombre de groupes et n le nombre total de valeurs des données. Le nombre de degrés de liberté pour le numérateur est inférieur de un au nombre de groupes, soit c – 1. Le nombre de degrés de liberté pour le dénominateur est le nombre total de valeurs de données, moins le nombre de groupes, soit n – c.
Il est clair que nous devons être très attentifs à savoir quelle est la procédure d’inférence avec laquelle nous travaillons. Cette connaissance nous permettra de connaître le nombre exact de degrés de liberté à utiliser.