Contents
La théorie des ensembles utilise un certain nombre d’opérations différentes pour construire de nouveaux ensembles à partir d’anciens. Il existe différentes façons de sélectionner certains éléments dans des ensembles donnés tout en en excluant d’autres. Le résultat est généralement un ensemble qui diffère des ensembles originaux. Il est important d’avoir des moyens bien définis pour construire ces nouveaux ensembles, par exemple l’union, l’intersection et la différence de deux ensembles. Une opération d’ensemble peut-être moins bien connue est appelée la différence symétrique.
Définition de la différence symétrique
Pour comprendre la définition de la différence symétrique, nous devons d’abord comprendre le mot « ou ». Bien que petit, le mot « or » a deux usages différents dans la langue anglaise. Il peut être exclusif ou inclusif (et il vient d’être utilisé exclusivement dans cette phrase). Si l’on nous dit que nous pouvons choisir entre A ou B, et que le sens est exclusif, alors nous n’avons peut-être que l’une des deux options. Si le sens est inclusif, alors nous pouvons avoir A, nous pouvons avoir B, ou nous pouvons avoir à la fois A et B.
En général, le contexte nous guide lorsque nous nous heurtons au mot ou et nous n’avons même pas besoin de réfléchir à la manière dont il est utilisé. Si on nous demande si nous voulons de la crème ou du sucre dans notre café, il est clairement sous-entendu que nous pouvons avoir les deux. En mathématiques, nous voulons éliminer toute ambiguïté. Ainsi, le mot « ou » en mathématiques a un sens inclusif.
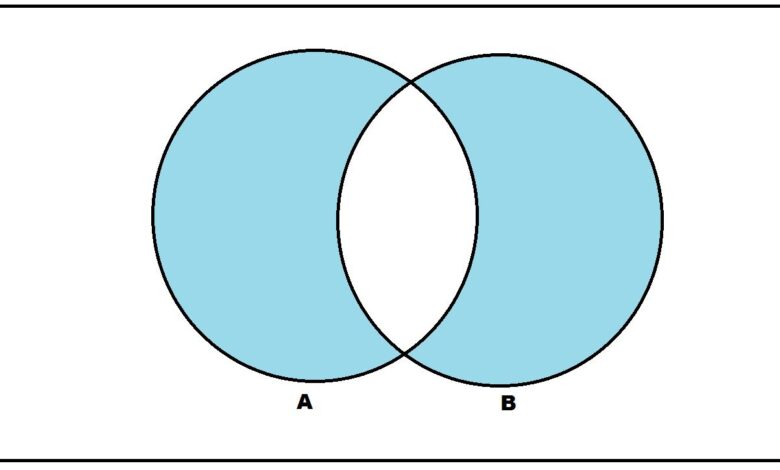
Le mot « ou » est donc employé au sens large dans la définition de l’union. L’union des ensembles A et B est l’ensemble des éléments de A ou B (y compris les éléments qui se trouvent dans les deux ensembles). Mais il devient intéressant d’avoir une opération d’ensemble qui construit l’ensemble contenant les éléments dans A ou B, où « ou » est utilisé au sens exclusif. C’est ce que nous appelons la différence symétrique. La différence symétrique des ensembles A et B sont les éléments de A ou B, mais pas de A et B. Bien que la notation varie pour la différence symétrique, nous l’écrivons A ∆ B
Pour un exemple de différence symétrique, nous considérerons les ensembles A = {1,2,3,4,5} et B = {2,4,6}. La différence symétrique entre ces ensembles est {1,3,5,6}.
En ce qui concerne les autres opérations de l’ensemble
D’autres opérations d’ensemble peuvent être utilisées pour définir la différence symétrique. D’après la définition ci-dessus, il est clair que nous pouvons exprimer la différence symétrique de A et B comme la différence de l’union de A et B et l’intersection de A et B. En symboles, nous écrivons : A ∆ B = (A ∪ B) – (A ∩ B).
Une expression équivalente, utilisant quelques opérations d’ensemble différentes, aide à expliquer la différence symétrique du nom. Plutôt que d’utiliser la formulation ci-dessus, nous pouvons écrire la différence symétrique comme suit : (A – B ) ∪ (B – A). Ici, nous voyons à nouveau que la différence symétrique est l’ensemble des éléments dans A mais pas dans B, ou dans B mais pas dans A. Nous avons donc exclu ces éléments à l’intersection de A et de B. Il est possible de prouver mathématiquement que ces deux formules sont équivalentes et se réfèrent au même ensemble.
La différence symétrique des noms
Le nom de différence symétrique suggère un lien avec la différence de deux ensembles. Cette différence d’ensemble est évidente dans les deux formules ci-dessus. Dans chacune d’elles, une différence de deux ensembles a été calculée. Ce qui distingue la différence symétrique de la différence, c’est sa symétrie. Par construction, les rôles de A et B peuvent être modifiés. Ce n’est pas le cas pour la différence entre deux ensembles.
Pour souligner ce point, avec un peu de travail, nous verrons la symétrie de la différence symétrique puisque nous voyons A ∆ B = (A – B ) ∪ (B – A) = (B – A) ∪ (A – B ) = B ∆ A.







