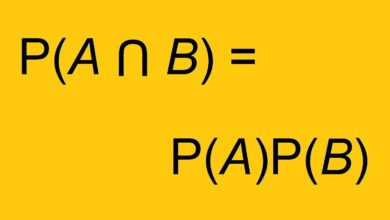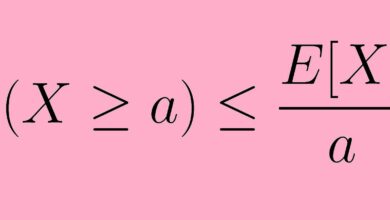Contents
La collecte de tous les résultats possibles d’une expérience de probabilité forme un ensemble connu sous le nom d’espace d’échantillonnage.
La probabilité se rapporte à des phénomènes aléatoires ou à des expériences de probabilité. Ces expériences sont toutes de nature différente et peuvent concerner des choses aussi diverses que le lancement de dés ou le retournement de pièces. Le fil conducteur de ces expériences de probabilité est qu’il existe des résultats observables. Le résultat se produit de manière aléatoire et est inconnu avant la réalisation de notre expérience.
Dans cette formulation de la théorie des ensembles de probabilités, l’espace d’échantillonnage d’un problème correspond à un ensemble important. Comme l’espace d’échantillonnage contient tous les résultats possibles, il forme un ensemble de tout ce que nous pouvons considérer. L’espace d’échantillonnage devient donc l’ensemble universel utilisé pour une expérience de probabilité particulière.
Espaces d’échantillons communs
Les espaces d’échantillonnage abondent et sont en nombre infini. Mais il y en a quelques-uns qui sont fréquemment utilisés à titre d’exemple dans une introduction aux statistiques ou un cours de probabilité. Vous trouverez ci-dessous les expériences et leurs espaces d’échantillons correspondants :
- Pour l’expérience de lancer une pièce de monnaie, l’espace d’échantillonnage est {Tête, Pile}. Il y a deux éléments dans cet espace.
- Pour l’expérience de retournement de deux pièces, l’espace d’échantillonnage est {(Pile, Face), (Pile, Face), (Pile, Face), (Pile, Face) }. Cet espace échantillon comporte quatre éléments.
- Pour l’expérience de retournement de trois pièces, l’espace d’échantillonnage est {(Pile, Face, Face), (Pile, Face, Face), (Pile, Face, Face), (Pile, Face, Face), (Pile, Face, Face), (Pile, Face, Face), (Pile, Pile, Face), (Pile, Pile, Pile) }. Cet espace d’échantillonnage comporte huit éléments.
- Pour l’expérience consistant à retourner n pièces de monnaie, où n est un nombre entier positif, l’espace d’échantillonnage est constitué de 2n éléments. Il existe un total de C (n, k) façons d’obtenir k têtes et n – k queues pour chaque nombre k de 0 à n.
- Pour l’expérience consistant à faire rouler un seul dé à six faces, l’espace d’échantillonnage est {1, 2, 3, 4, 5, 6}
- Pour l’expérience consistant à lancer deux dés à six faces, l’espace d’échantillonnage est constitué de l’ensemble des 36 paires possibles des nombres 1, 2, 3, 4, 5 et 6.
- Pour l’expérience consistant à lancer trois dés à six faces, l’espace d’échantillonnage est constitué par l’ensemble des 216 triples possibles des nombres 1, 2, 3, 4, 5 et 6.
- Pour l’expérience de lancer n dés à six faces, où n est un nombre entier positif, l’espace d’échantillonnage est constitué de 6n éléments.
- Pour une expérience de dessin à partir d’un jeu de cartes standard, l’espace d’échantillonnage est l’ensemble qui énumère les 52 cartes d’un jeu. Pour cet exemple, l’espace d’échantillonnage ne peut prendre en compte que certaines caractéristiques des cartes, telles que le rang ou la couleur.
Création d’autres espaces d’échantillonnage
La liste ci-dessus comprend certains des espaces échantillons les plus couramment utilisés. D’autres sont là pour différentes expériences. Il est également possible de combiner plusieurs des expériences ci-dessus. Dans ce cas, nous obtenons un espace échantillon qui est le produit cartésien de nos espaces échantillons individuels. Nous pouvons également utiliser un diagramme en arbre pour former ces espaces échantillons.
Par exemple, nous pouvons vouloir analyser une expérience de probabilité dans laquelle nous lançons d’abord une pièce de monnaie, puis un dé. Comme il y a deux résultats pour le tirage à pile ou face et six résultats pour le lancer de dé, il y a un total de 2 x 6 = 12 résultats dans l’espace échantillon que nous considérons.