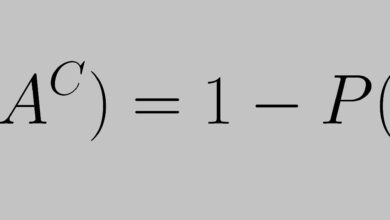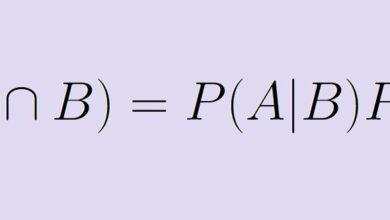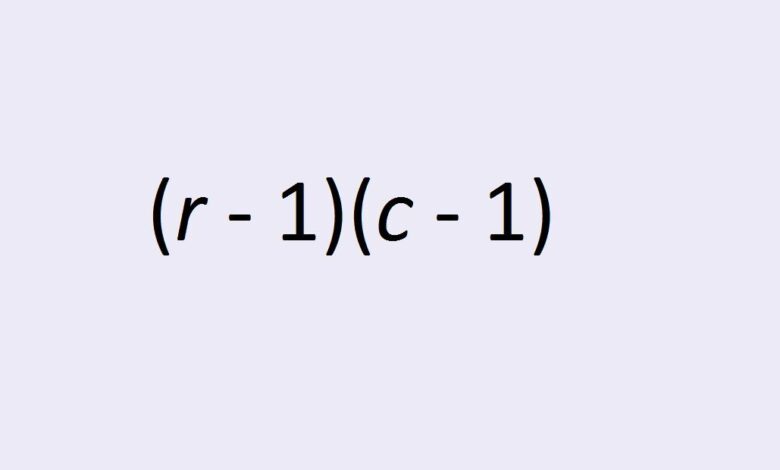
Contents
Le nombre de degrés de liberté pour l’indépendance de deux variables catégorielles est donné par une formule simple : (r – 1)(c – 1). Ici, r est le nombre de lignes et c est le nombre de colonnes dans le tableau bidirectionnel des valeurs de la variable catégorielle. Lisez ce qui suit pour en savoir plus sur ce sujet et pour comprendre pourquoi cette formule donne le nombre correct.
Contexte
Une étape du processus de nombreux tests d’hypothèses est la détermination du nombre de degrés de liberté. Ce nombre est important car pour les distributions de probabilités qui impliquent une famille de distributions, comme la distribution du chi carré, le nombre de degrés de liberté permet de déterminer la distribution exacte de la famille que nous devrions utiliser dans notre test d’hypothèse.
Les degrés de liberté représentent le nombre de choix libres que nous pouvons faire dans une situation donnée. L’un des tests d’hypothèse qui nous oblige à déterminer les degrés de liberté est le test du chi carré pour l’indépendance de deux variables catégorielles.
Tests d’indépendance et tables à double sens
Le test du chi carré pour l’indépendance exige que nous construisions un tableau à double sens, également appelé tableau de contingence. Ce type de tableau comporte r lignes et c colonnes, représentant les r niveaux d’une variable catégorielle et les c niveaux de l’autre variable catégorielle. Ainsi, si nous ne comptons pas la ligne et la colonne dans lesquelles nous enregistrons les totaux, il y a un total de cellules rc dans le tableau à double entrée.
Le test du chi carré pour l’indépendance nous permet de tester l’hypothèse selon laquelle les variables catégorielles sont indépendantes les unes des autres. Comme nous l’avons mentionné ci-dessus, les lignes r et les colonnes c du tableau nous donnent (r – 1)(c – 1) degrés de liberté. Mais il n’est peut-être pas évident de comprendre immédiatement pourquoi il s’agit du nombre correct de degrés de liberté.
Le nombre de degrés de liberté
Pour savoir pourquoi (r – 1)(c – 1) est le chiffre correct, nous allons examiner cette situation plus en détail. Supposons que nous connaissions les totaux marginaux pour chacun des niveaux de nos variables catégorielles. En d’autres termes, nous connaissons le total de chaque ligne et le total de chaque colonne. Pour la première ligne, il y a c colonnes dans notre tableau, donc c cellules. Une fois que nous connaissons les valeurs de toutes ces cellules sauf une, alors parce que nous connaissons le total de toutes les cellules, il s’agit d’un simple problème d’algèbre pour déterminer la valeur de la cellule restante. Si nous remplissions ces cellules de notre tableau, nous pourrions entrer librement c – 1 d’entre elles, mais alors la cellule restante est déterminée par le total de la ligne. Il y a donc c – 1 degrés de liberté pour la première rangée.
Nous continuons de cette manière pour la ligne suivante, et il y a de nouveau c – 1 degrés de liberté. Ce processus se poursuit jusqu’à ce que nous arrivions à l’avant-dernière rangée. Chacune des rangées, à l’exception de la dernière, contribue à c – 1 degrés de liberté au total. Lorsque nous avons toutes les lignes sauf la dernière, nous pouvons déterminer toutes les entrées de la dernière ligne parce que nous connaissons la somme des colonnes. Cela nous donne r – 1 lignes avec c – 1 degrés de liberté dans chacune d’entre elles, pour un total de (r – 1)(c – 1) degrés de liberté.
Exemple
Nous le voyons dans l’exemple suivant. Supposons que nous ayons un tableau à double sens avec deux variables catégorielles. Une variable a trois niveaux et l’autre en a deux. Supposons en outre que nous connaissions les totaux des lignes et des colonnes de ce tableau :
Niveau A
Niveau B
Total
Niveau 1
100
Niveau 2
200
Niveau 3
300
Total
200
400
600
La formule prévoit qu’il y a (3-1)(2-1) = 2 degrés de liberté. Nous voyons cela comme suit. Supposons que nous remplissions la cellule supérieure gauche avec le nombre 80. Cela déterminera automatiquement toute la première ligne d’entrées :
Niveau A
Niveau B
Total
Niveau 1
80
20
100
Niveau 2
200
Niveau 3
300
Total
200
400
600
Maintenant, si nous savons que la première entrée de la deuxième ligne est 50, alors le reste du tableau est rempli, car nous connaissons le total de chaque ligne et colonne :
Niveau A
Niveau B
Total
Niveau 1
80
20
100
Niveau 2
50
150
200
Niveau 3
70
230
300
Total
200
400
600
Le tableau est entièrement rempli, mais nous n’avions que deux choix libres. Une fois ces valeurs connues, le reste du tableau a été entièrement déterminé.
Bien que nous n’ayons généralement pas besoin de savoir pourquoi il y a autant de degrés de liberté, il est bon de savoir que nous appliquons vraiment le concept de degrés de liberté à une nouvelle situation.