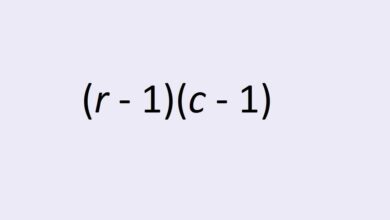
Contents
L’analyse factorielle de la variance, également appelée ANOVA, nous permet d’effectuer des comparaisons multiples de plusieurs moyennes de population. Plutôt que de le faire par paires, nous pouvons examiner simultanément toutes les moyennes considérées. Pour effectuer un test ANOVA, nous devons comparer deux types de variation, la variation entre les moyennes de l’échantillon, ainsi que la variation au sein de chacun de nos échantillons.
Nous combinons toutes ces variations en une seule statistique, appelée statistique F car elle utilise la distribution F. Nous le faisons en divisant la variation entre les échantillons par la variation au sein de chaque échantillon. La manière de procéder est généralement gérée par un logiciel, mais il est utile de voir un tel calcul effectué.
Il sera facile de se perdre dans ce qui suit. Voici la liste des étapes que nous allons suivre dans l’exemple ci-dessous :
- Calculer la moyenne de l’échantillon pour chacun de nos échantillons ainsi que la moyenne de toutes les données de l’échantillon.
- Calculez la somme des carrés d’erreur. Ici, dans chaque échantillon, nous élevons au carré l’écart de chaque valeur de données par rapport à la moyenne de l’échantillon. La somme de tous les écarts au carré est la somme des carrés d’erreur, abrégée ESS.
- Calculer la somme des carrés de traitement. Nous élevons au carré l’écart de la moyenne de chaque échantillon par rapport à la moyenne globale. La somme de tous ces carrés d’écart est multipliée par un de moins que le nombre d’échantillons dont nous disposons. Ce nombre est la somme des carrés de traitement, en abrégé SST.
- Calculer les degrés de liberté. Le nombre total de degrés de liberté est inférieur d’une unité au nombre total de points de données de notre échantillon, soit n – 1. Le nombre de degrés de liberté de traitement est inférieur d’une unité au nombre d’échantillons utilisés, soit m – 1. Le nombre de degrés de liberté d’erreur est le nombre total de points de données, moins le nombre d’échantillons, soit n – m.
- Calculer le carré moyen de l’erreur. Il est désigné par MSE = SSE/(n – m).
- Calculer le carré moyen du traitement. Il est désigné par MST = SST/m – `1.
- Calculer la statistique F. C’est le rapport des deux carrés moyens que nous avons calculés. Donc F = MST/MSE.
Les logiciels font tout cela assez facilement, mais il est bon de savoir ce qui se passe en coulisses. Dans ce qui suit, nous élaborons un exemple d’ANOVA en suivant les étapes énumérées ci-dessus.
Données et moyens d’échantillonnage
Supposons que nous ayons quatre populations indépendantes qui remplissent les conditions pour une ANOVA à facteur unique. Nous souhaitons tester l’hypothèse nulle H0 : μ1 = μ2 = μ3 = μ4. Pour les besoins de cet exemple, nous utiliserons un échantillon de taille trois de chacune des populations étudiées. Les données de nos échantillons sont les suivantes :
- Échantillon de la population n° 1 : 12, 9, 12. La moyenne de l’échantillon est de 11.
- Échantillon de la population n° 2 : 7, 10, 13. La moyenne de l’échantillon est de 10.
- Échantillon de la population n° 3 : 5, 8, 11. La moyenne de l’échantillon est de 8.
- Échantillon de la population n° 4 : 5, 8, 8. La moyenne de l’échantillon est de 7.
La moyenne de l’ensemble des données est de 9.
Somme des carrés d’erreur
Nous calculons maintenant la somme des carrés des écarts par rapport à la moyenne de chaque échantillon. C’est ce qu’on appelle la somme des carrés d’erreur.
- Pour l’échantillon de la population n° 1 : (12 – 11)2 + (9 – 11)2 +(12 – 11)2 = 6
- Pour l’échantillon de la population n°2 : (7 – 10)2 + (10- 10)2 +(13 – 10)2 = 18
- Pour l’échantillon de la population n° 3 : (5 – 8)2 + (8 – 8)2 +(11 – 8)2 = 18
- Pour l’échantillon de la population n° 4 : (5 – 7)2 + (8 – 7)2 +(8 – 7)2 = 6.
Nous additionnons ensuite toutes ces sommes d’écarts au carré et obtenons 6 + 18 + 18 + 6 = 48.
Somme des carrés de traitement
Nous calculons maintenant la somme des carrés de traitement. Nous examinons ici les écarts au carré de la moyenne de chaque échantillon par rapport à la moyenne globale, et nous multiplions ce nombre par un de moins que le nombre de populations :
3[(11 – 9)2 + (10 – 9)2 +(8 – 9)2 + (7 – 9)2] = 3[4 + 1 + 1 + 4] = 30.
Degrés de liberté
Avant de passer à l’étape suivante, nous avons besoin des degrés de liberté. Il y a 12 valeurs de données et quatre échantillons. Ainsi, le nombre de degrés de liberté de traitement est de 4 – 1 = 3. Le nombre de degrés de liberté d’erreur est de 12 – 4 = 8.
Carrés moyens
Nous divisons maintenant notre somme de carrés par le nombre approprié de degrés de liberté afin d’obtenir les carrés moyens.
- Le carré moyen du traitement est de 30 / 3 = 10.
- Le carré moyen de l’erreur est de 48 / 8 = 6.
La statistique F
La dernière étape consiste à diviser le carré moyen de traitement par le carré moyen d’erreur. Il s’agit de la statistique F des données. Ainsi, dans notre exemple, F = 10/6 = 5/3 = 1,667.
Des tableaux de valeurs ou des logiciels peuvent être utilisés pour déterminer la probabilité d’obtenir une valeur de la statistique F aussi extrême que cette valeur par le seul hasard.