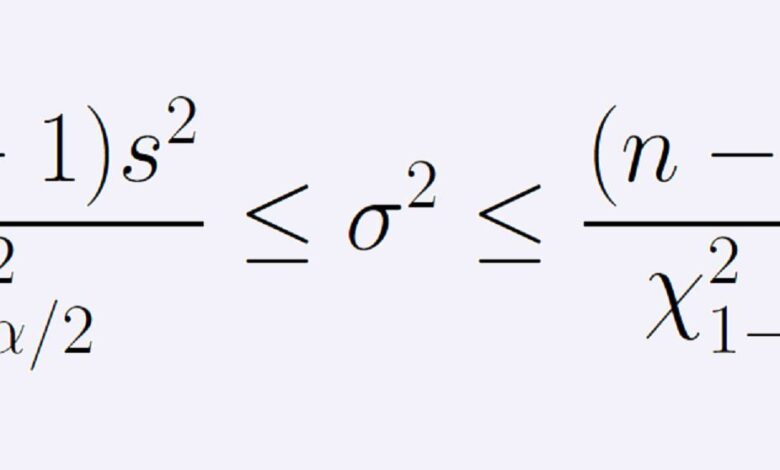
Contents
La variance de la population donne une indication sur la manière de répartir un ensemble de données. Malheureusement, il est généralement impossible de savoir exactement quel est ce paramètre de population. Pour compenser notre manque de connaissance, nous utilisons un sujet issu des statistiques inférentielles appelé intervalles de confiance. Nous allons voir un exemple de calcul d’un intervalle de confiance pour une variance de population.
Formule de l’intervalle de confiance
La formule de l’intervalle de confiance (1 – α) concernant la variance de la population. est donnée par la chaîne d’inégalités suivante :
[ (n – 1)s2] / B < σ2 < [ (n - 1)s2] / A. Ici, n est la taille de l'échantillon, s2 est la variance de l'échantillon. Le nombre A est le point de la distribution du chi carré avec n -1 degrés de liberté où exactement α/2 de l'aire sous la courbe est à gauche de A. De la même manière, le nombre B est le point de la même distribution du chi carré avec exactement α/2 de l'aire sous la courbe à droite de B.Préliminaires
Nous commençons par un ensemble de données comportant 10 valeurs. Cet ensemble de valeurs a été obtenu par un simple échantillon aléatoire :
97, 75, 124, 106, 120, 131, 94, 97,96, 102
Une analyse exploratoire des données serait nécessaire pour montrer qu’il n’y a pas de valeurs aberrantes. En construisant un diagramme à tiges et à feuilles, nous voyons que ces données proviennent probablement d’une distribution qui est à peu près normalement distribuée. Cela signifie que nous pouvons procéder à la recherche d’un intervalle de confiance de 95% pour la variance de la population.
Variance de l’échantillon
Nous devons estimer la variance de la population avec la variance de l’échantillon, désignée par s2. Nous commençons donc par calculer cette statistique. En gros, nous faisons la moyenne de la somme des écarts au carré par rapport à la moyenne. Cependant, plutôt que de diviser cette somme par n, nous la divisons par n – 1.
Nous constatons que la moyenne de l’échantillon est de 104,2. Nous avons donc la somme des carrés des écarts par rapport à la moyenne donnée par :
(97 – 104.2)2 + (75 – 104.3)2 + . . . + (96 – 104.2)2 + (102 – 104.2)2 = 2495.6
Nous divisons cette somme par 10 – 1 = 9 pour obtenir une variance d’échantillon de 277.
Distribution du chi carré
Nous passons maintenant à notre distribution du chi carré. Comme nous avons 10 valeurs de données, nous avons 9 degrés de liberté. Comme nous voulons le milieu de notre distribution à 95 %, nous avons besoin de 2,5 % dans chacune des deux queues. Nous consultons un tableau du chi carré ou un logiciel et nous constatons que les valeurs de 2,7004 et 19,023 du tableau englobent 95 % de la surface de la distribution. Ces chiffres sont respectivement A et B.
Nous avons maintenant tout ce dont nous avons besoin, et nous sommes prêts à assembler notre intervalle de confiance. La formule pour l’extrémité gauche est la suivante [ (n – 1)s2] / B. Cela signifie que notre extrémité gauche est :
(9 x 277)/19.023 = 133
On trouve l’extrémité droite en remplaçant B par A :
(9 x 277)/2.7004 = 923
Nous sommes donc convaincus à 95 % que l’écart de population se situe entre 133 et 923.
Écart-type de la population
Bien sûr, puisque l’écart-type est la racine carrée de la variance, cette méthode pourrait être utilisée pour construire un intervalle de confiance pour l’écart-type de la population. Il suffirait de prendre la racine carrée des paramètres. Le résultat serait un intervalle de confiance de 95% pour l’écart type.