Contents
Une question qu’il est toujours important de se poser en matière de statistiques est la suivante : « Le résultat observé est-il dû au seul hasard ou est-il statistiquement significatif ? Une classe de tests d’hypothèse, appelés tests de permutation, nous permet de tester cette question. La vue d’ensemble et les étapes d’un tel test sont :
- Nous avons divisé nos sujets en un groupe de contrôle et un groupe expérimental. L’hypothèse nulle est qu’il n’y a pas de différence entre ces deux groupes.
- Appliquer un traitement au groupe expérimental.
- Mesurer la réponse au traitement
- Tenez compte de toutes les configurations possibles du groupe expérimental et de la réponse observée.
- Calculer une valeur p basée sur notre réponse observée par rapport à tous les groupes expérimentaux potentiels.
Il s’agit d’une ébauche de permutation. Pour étoffer ce schéma, nous allons passer du temps à examiner en détail un exemple élaboré d’un tel test de permutation.
Exemple
Supposons que nous étudions les souris. Nous nous intéressons en particulier à la rapidité avec laquelle les souris terminent un labyrinthe qu’elles n’ont jamais rencontré auparavant. Nous souhaitons apporter des preuves en faveur d’un traitement expérimental. L’objectif est de démontrer que les souris du groupe de traitement résoudront le labyrinthe plus rapidement que les souris non traitées.
Nous commençons par nos sujets : six souris. Par commodité, les souris seront désignées par les lettres A, B, C, D, E, F. Trois de ces souris doivent être choisies au hasard pour le traitement expérimental, et les trois autres sont placées dans un groupe de contrôle dans lequel les sujets reçoivent un placebo.
Nous allons ensuite choisir au hasard l’ordre dans lequel les souris sont sélectionnées pour parcourir le labyrinthe. Le temps passé à terminer le labyrinthe pour toutes les souris sera noté, et une moyenne de chaque groupe sera calculée.
Supposons que notre sélection aléatoire comporte les souris A, C et E dans le groupe expérimental, avec les autres souris dans le groupe de contrôle placebo. Une fois le traitement mis en œuvre, nous choisissons au hasard l’ordre dans lequel les souris vont parcourir le labyrinthe.
Les temps de parcours pour chacune des souris sont :
- La souris A fait la course en 10 secondes
- La souris B fait la course en 12 secondes
- La souris C fait la course en 9 secondes
- La souris D fait la course en 11 secondes
- La souris E fait la course en 11 secondes
- La souris F fait la course en 13 secondes.
Le temps moyen pour compléter le labyrinthe pour les souris du groupe expérimental est de 10 secondes. Le temps moyen pour compléter le labyrinthe pour les souris du groupe de contrôle est de 12 secondes.
Nous pourrions poser quelques questions. Le traitement est-il vraiment à l’origine du délai moyen plus court ? Ou avons-nous simplement eu de la chance dans notre sélection du groupe de contrôle et du groupe expérimental ? Le traitement peut n’avoir eu aucun effet et nous avons choisi au hasard les souris les plus lentes pour recevoir le placebo et les souris les plus rapides pour recevoir le traitement. Un test de permutation nous aidera à répondre à ces questions.
Hypothèses
Les hypothèses de notre test de permutation sont les suivantes :
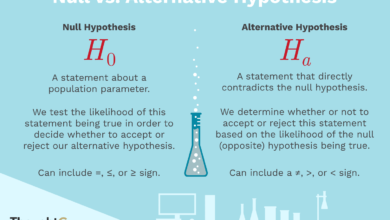
- L’hypothèse nulle est l’affirmation de l’absence d’effet. Pour ce test spécifique, nous avons H0 : il n’y a pas de différence entre les groupes de traitement. Le temps moyen pour parcourir le labyrinthe pour toutes les souris sans traitement est le même que le temps moyen pour toutes les souris avec le traitement.
- L’hypothèse alternative est celle pour laquelle nous essayons d’établir des preuves en faveur. Dans ce cas, nous aurions Ha : le temps moyen pour toutes les souris avec le traitement sera plus rapide que le temps moyen pour toutes les souris sans le traitement.
Permutations
Il y a six souris, et trois places dans le groupe expérimental. Cela signifie que le nombre de groupes expérimentaux possibles est donné par le nombre de combinaisons C(6,3) = 6!/(3!3 !) = 20. Les individus restants feraient partie du groupe de contrôle. Il existe donc 20 façons différentes de choisir au hasard des individus dans nos deux groupes.
L’affectation de A, C et E au groupe expérimental a été faite de manière aléatoire. Comme il existe 20 configurations de ce type, celle qui comporte A, C et E dans le groupe expérimental a une probabilité de 1/20 = 5 % de se produire.
Nous devons déterminer les 20 configurations du groupe expérimental des individus de notre étude.
- Groupe expérimental : A B C et groupe de contrôle : D E F
- Groupe expérimental : A B D et groupe de contrôle : C E F
- Groupe expérimental : A B E et groupe de contrôle : C D F
- Groupe expérimental : A B F et groupe de contrôle : C D E
- Groupe expérimental : A C D et groupe de contrôle : B E F
- Groupe expérimental : A C E et groupe de contrôle : B D F
- Groupe expérimental : A C F et groupe de contrôle : B D E
- Groupe expérimental : A D E et groupe de contrôle : B C F
- Groupe expérimental : A D F et groupe de contrôle : B C E
- Groupe expérimental : A E F et groupe de contrôle : B C D
- Groupe expérimental : B C D et groupe de contrôle : A E F
- Groupe expérimental : B C E et groupe de contrôle : A D F
- Groupe expérimental : B C F et groupe de contrôle : A D E
- Groupe expérimental : B D E et groupe de contrôle : A C F
- Groupe expérimental : B D F et groupe de contrôle : A C E
- Groupe expérimental : B E F et groupe de contrôle : A C D
- Groupe expérimental : C D E et groupe de contrôle : A B F
- Groupe expérimental : C D F et groupe de contrôle : A B E
- Groupe expérimental : C E F et groupe de contrôle : A B D
- Groupe expérimental : D E F et groupe de contrôle : A B C
Nous examinons ensuite chaque configuration des groupes expérimentaux et de contrôle. Nous calculons la moyenne pour chacune des 20 permutations dans la liste ci-dessus. Par exemple, pour la première, A, B et C ont des temps de 10, 12 et 9, respectivement. La moyenne de ces trois nombres est de 10,3333. Toujours dans cette première permutation, D, E et F ont des temps de 11, 11 et 13, respectivement. La moyenne de ces trois nombres est de 11,6666.
Après avoir calculé la moyenne de chaque groupe, nous calculons la différence entre ces moyennes. Chacun des éléments suivants correspond à la différence entre le groupe expérimental et le groupe témoin qui ont été énumérés ci-dessus.
- Placebo – Traitement = 1,33333333333 secondes
- Placebo – Traitement = 0 seconde
- Placebo – Traitement = 0 seconde
- Placebo – Traitement = -1,33333333333 secondes
- Placebo – Traitement = 2 secondes
- Placebo – Traitement = 2 secondes
- Placebo – Traitement = 0,666666667 secondes
- Placebo – Traitement = 0,666666667 secondes
- Placebo – Traitement = -0,666666667 secondes
- Placebo – Traitement = -0,666666667 secondes
- Placebo – Traitement = 0,666666667 secondes
- Placebo – Traitement = 0,666666667 secondes
- Placebo – Traitement = -0,666666667 secondes
- Placebo – Traitement = -0,666666667 secondes
- Placebo – Traitement = -2 secondes
- Placebo – Traitement = -2 secondes
- Placebo – Traitement = 1,33333333333 secondes
- Placebo – Traitement = 0 seconde
- Placebo – Traitement = 0 seconde
- Placebo – Traitement = -1,33333333333 secondes
P-Value
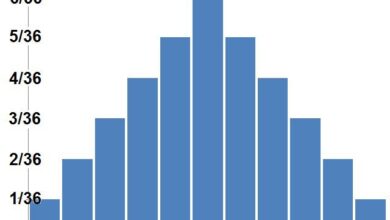
Maintenant, nous classons les différences entre les moyennes de chaque groupe que nous avons notées ci-dessus. Nous calculons également le pourcentage de nos 20 configurations différentes qui sont représentées par chaque différence de moyenne. Par exemple, quatre des 20 n’avaient aucune différence entre les moyennes des groupes de contrôle et de traitement. Cela représente 20 % des 20 configurations mentionnées ci-dessus.
- -2 pour 10
- -1,33 pour 10
- -0,667 pour 20%.
- 0 pour 20
- 0,667 pour 20%.
- 1,33 pour 10
- 2 pour 10 %.
Nous comparons ici cette liste à notre résultat observé. Notre sélection aléatoire de souris pour les groupes de traitement et de contrôle a donné une différence moyenne de 2 secondes. Nous constatons également que cette différence correspond à 10 % de tous les échantillons possibles. Le résultat est que pour cette étude, nous avons une valeur p de 10 %.