Contents
Le Cambridge English Dictionary définit la géométrie comme « le domaine des mathématiques relatif à l’étude de l’espace et aux relations entre points, droites, courbes et surfaces ». Cette définition s’accorde parfaitement avec l’étude académique de la géométrie, qui est basée sur le rationalisme. On a cependant fait valoir qu’il existe un côté opposé mais complémentaire à ce domaine d’étude. Selon ce point de vue, la géométrie a un côté intuitif et certaines formes et proportions géométriques contiennent une signification sacrée. Cette croyance peut être considérée comme la base de la géométrie sacrée. Le concept et l’application de la géométrie sacrée se retrouvent dans de nombreuses civilisations à travers le monde.
Géométrie ancienne : Le développement de la géométrie dans différentes cultures
On pense généralement que la géométrie a commencé comme un sujet pratique et qu’elle est née de préoccupations quotidiennes. Les premiers praticiens de la géométrie ont élaboré un ensemble de règles pour calculer les longueurs, les surfaces et les volumes. Toutefois, nombre d’entre elles étaient des approximations grossières, basées sur des essais et des erreurs. Selon Hérodote, la géométrie a été établie par les anciens Egyptiens . Cela est confirmé par des preuves écrites provenant de l’Égypte elle-même. Néanmoins, les anciens Mésopotamiens sont également connus pour avoir pratiqué la géométrie, tout comme les anciens Chinois et les Indiens.
Euclide est considéré comme le père de la géométrie. Elements, dont un fragment est montré ici, est l’un des ouvrages les plus influents de l’histoire des mathématiques. ( Domaine public )
Vers le VIe siècle avant J.-C., les Grecs se sont impliqués dans la géométrie, la transformant d’un sujet pratique en un sujet abstrait basé sur des généralisations. C’est également des Grecs que cette branche des mathématiques a obtenu son nom, car elle est une combinaison de deux mots grecs, géo (terre) et métron (mesure). Bien que de nombreux penseurs grecs et romains aient contribué à ce sujet, aucun n’a eu un impact plus important qu’Euclide, qui est souvent considéré comme le père de la géométrie. Euclide a vécu à Alexandrie entre le IVe et le IIIe siècle avant J.-C., et est surtout connu pour ses Éléments. Ce traité est considéré comme l’un des ouvrages les plus influents de l’histoire des mathématiques. Bien que l’on pense généralement qu’il ne contient que de la géométrie, les Éléments d’Euclide traitent également d’autres domaines des mathématiques, à savoir la théorie des nombres élémentaires et les lignes incommensurables.
Euclid’s Elements est un bon exemple de l’approche rationnelle et académique de l’étude de la géométrie. Comme mentionné précédemment, d’autres penseurs du monde classique ont contribué à l’étude de la géométrie, dont certains ont adopté une approche différente de ce sujet. Ces penseurs voyaient dans la géométrie des significations symboliques et sacrées, et leur domaine d’étude peut donc être qualifié de géométrie sacrée. Un groupe de ces penseurs était les Pythagoriciens, dont l’école de philosophie a été fondée par Pythagore de Samos .
Théorème de Pythagore : La plus belle équation mathématique du monde
Aujourd’hui, Pythagore est surtout connu pour le Théorème de Pythagore (également appelé Théorème de Pythagore), qui stipule que « la somme des carrés des jambes d’un triangle droit est égale au carré de l’hypoténuse (le côté opposé à l’angle droit) ». Bien que nommé d’après le philosophe grec, le théorème est en fait beaucoup plus ancien. Par exemple, plusieurs tablettes d’argile babyloniennes datant de 1900 à 1600 avant J.-C. témoignent d’une certaine connaissance du théorème, et sont également mentionnées dans les Shulba Sutras indiens, écrits entre 800 et 400 avant J.-C. Néanmoins, l’association de ce théorème avec les Pythagoriciens est quelque peu pertinente, car ils semblent avoir été particulièrement intéressés par les triangles.
Pythagoriciens célébrant le lever du soleil, dans un tableau de 1869 de Fyodor Bronnikov. ( Domaine public )
Il n’est donc pas étonnant que les Pythagoriciens aient inventé un symbole triangulaire en géométrie sacrée, connu sous le nom de tétractys, ou tétractys de la décade (« tétractys » signifiant « quatre », et « décade » signifiant « dix »). Ce symbole se compose de dix points disposés sur quatre rangées, formant ainsi un triangle équilatéral. Le tétracty est plein de sens symbolique. Par exemple, chaque rangée de points est censée contenir une signification cachée. La première rangée, qui ne comporte qu’un seul point, représenterait le principe actif, ou la puissance divine derrière toute la création ; la deuxième, le principe passif, ou la matière ; la troisième, le monde issu de l’union des principes actifs et passifs ; et la quatrième, les quatre arts et sciences libéraux qui complètent le monde.
Naturellement, le tétractyle a été adopté par les Pythagoriciens comme leur symbole. Dans l’école d’Athènes de Raphaël, Pythagore est représenté à côté d’Archimède, qui tient une tablette. La partie supérieure de la tablette représente le principe d’Archimède, tandis que la partie inférieure représente les tétractyles, un clin d’œil aux Pythagoriciens. Les tétractyles n’étaient cependant pas un symbole purement pythagoricien, et qu’ils avaient également une influence sur la géométrie sacrée d’autres cultures. Il a été souligné, par exemple, que les quatre lettres du Tétragramme (le nom biblique du Dieu d’Israël) peuvent être disposées comme des tétractyes.
La valeur symbolique des formes
Les Pythagoriciens, bien sûr, n’étaient pas les seuls à s’intéresser aux triangles. Par exemple, les fenêtres triangulaires sont courantes dans les églises chrétiennes. Dans ce contexte, cependant, le triangle est considéré comme représentant la Sainte Trinité. Autre exemple, les triangles ont également une valeur symbolique dans le mouvement New Age. Un triangle dirigé vers le haut, par exemple, peut représenter l’énergie masculine et l’ascension dans le monde spirituel, tandis qu’un triangle dirigé vers le bas représente l’énergie féminine et la descente dans le monde physique. Une combinaison de ces deux triangles, qui crée un hexagramme, peut être interprétée comme l’accomplissement de l’harmonie.
Manuscrit du XVe siècle montrant des penseurs occidentaux et arabes pratiquant la géométrie. ( Domaine public )
Outre le triangle, de nombreuses autres formes ont été imprégnées d’une signification symbolique, faisant ainsi partie de la géométrie sacrée. Comme le triangle, ces formes peuvent avoir des significations différentes selon le contexte dans lequel elles ont été produites. Le cercle, par exemple, se trouve dans diverses cultures du monde entier, et contient donc de multiples significations. Les Pythagoriciens, par exemple, percevaient le cercle comme un symbole d’unité, d’unicité et d’indivisibilité. Pour les bouddhistes zen, le cercle est un symbole d’illumination, tandis que les Chinois considéraient cette forme comme un symbole du ciel. En outre, le cercle est presque universellement utilisé comme symbole du Soleil. Dans l’astronomie moderne, ce corps céleste est représenté sous la forme d’un cercle avec un point au milieu.
Le cercle peut être répété afin de créer de nouveaux symboles. L’un d’entre eux, par exemple, est la vesica piscis (qui signifie littéralement « vessie de poisson »), qui est formée par l’intersection de deux cercles de même rayon. Les deux cercles se croisent de telle manière que le centre de chaque cercle touche le périmètre de l’autre. On dit que l’intersection de deux cercles dans la vesica piscis représente une compréhension mutuelle, une vision partagée, ou un terrain d’entente entre deux individus égaux. La vesica piscis peut à son tour être répétée afin de produire d’autres symboles.
Six vesica piscis disposées radialement autour d’un cercle central, ou six cercles s’ajustant autour d’un septième, tous de même rayon, produisent une rosette à six pétales, connue également sous le nom de Graine de vie. Comme ce symbole contient sept cercles, il a été interprété comme représentant la création. En répétant la rosette à six pétales, un autre symbole, la Fleur de Vie, peut être produit. La Fleur de Vie est un symbole ancien, et est représentée dans divers sites sacrés à travers le monde. Pour certains, ce symbole représente l’ordre divin et mathématique de l’Univers.
Beaucoup prétendent que la façade du Parthénon, qui fait partie de l’Acropole d’Athènes, a été conçue selon le nombre d’or. ( TTstudio / Adobe Stock )
À la recherche du rapport d’or
La géométrie sacrée implique également des proportions géométriques. L’une des plus connues est le nombre d’or, connu sous de nombreux autres noms, dont phi, la proportion divine, et la moyenne d’or. Le nombre d’or peut être défini comme suit :
« le rapport d’un segment de ligne coupé en deux morceaux de longueurs différentes de telle sorte que le rapport du segment entier à celui du segment le plus long soit égal au rapport du segment le plus long au segment le plus court ».
La coquille de nautile est un exemple populaire de proportion dorée dans la nature. ( CSIRO / CC PAR 3,0 )
En mathématiques, c’est un nombre irrationnel représenté par la lettre grecque φ (phi). Sa valeur est d’environ 1,618, dérivée de l’équation quadratique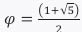 
. Bien que ce rapport ait été décrit pour la première fois par Euclide, il n’a été qualifié de « doré » que beaucoup plus tard, c’est-à-dire en 1835, lorsqu’il a été désigné comme tel par le mathématicien allemand Martin Ohm. D’ailleurs, c’est également au XIXe siècle que le ratio a reçu la lettre grecque φ pour le représenter. Cette lettre a été attribuée par un mathématicien américain, Mark Barr.
Apparemment, les anciens Grecs ont trouvé que le nombre d’or fournissait « la proportion la plus esthétique des côtés d’un rectangle », et sont supposés l’avoir appliqué dans leur architecture. On a prétendu, par exemple, que la façade du Parthénon à Athènes avait été conçue en utilisant le nombre d’or. Cela a été contesté, car il a été souligné, par exemple, que cette affirmation n’est pas étayée par des mesures réelles et que le Parthénon a été construit environ un siècle avant la naissance d’Euclide.
Leonardo da Vinvi aurait largement utilisé le nombre d’or dans ses œuvres. ( myper / Adobe Photo )
Le nombre d’or n’a atteint sa notoriété que pendant la Renaissance, bien après avoir été décrit pour la première fois par Euclide. En 1509, le mathématicien italien Luca Pacioli a écrit un livre intitulé De divina proportione (qui se traduit par « La proportion divine »), qui explorait le concept du nombre d’or. Ce livre a été illustré par Léonard de Vinci, qui aurait largement utilisé le nombre d’or dans ses travaux. L’homme de Vitruve du polymath, par exemple, est souvent présenté comme ayant été dessiné selon le nombre d’or, bien qu’il ait également été souligné qu’il n’existe aucune preuve concrète pour soutenir cette affirmation. Il a également été affirmé que le nombre d’or existe dans la nature, bien que cela ne soit pas entièrement vrai non plus. Un exemple populaire est la croissance de la coquille du nautile, dans laquelle on prétend que le nombre d’or peut être observé. Il a toutefois été souligné que la coquille se développe en « spirale qui tourne d’un angle constant sur toute sa longueur », et qu’un angle constant n’est pas égal au nombre d’or.
Le nombre d’or est discernable dans des œuvres d’art comme la Joconde de Léonard. ( Domaine public )
En tout état de cause, le nombre d’or est un concept significatif de la géométrie sacrée, et il est censé apparaître à la fois dans la nature et dans les œuvres de l’homme. La Grande Pyramide, les compositions musicales de Mozart et la croissance des plantes suivraient toutes le nombre d’or. En conséquence, ce rapport a été imprégné d’une valeur symbolique. Par exemple, il a été dit que le nombre d’or « relie symboliquement chaque nouvelle génération à ses ancêtres, préservant la continuité de la relation comme moyen de retracer sa lignée ».
Les solides de Platon et la théorie de l’univers de Platon
Les solides, c’est-à-dire les formes tridimensionnelles, ont également leur place dans la géométrie sacrée. Les solides les plus couramment mentionnés dans la géométrie sacrée sont les solides dits de Platon . Bien que Platon n’ait pas créé ces solides lui-même, ils portent son nom, comme il le mentionne dans son dialogue Timée. Dans cet ouvrage, le philosophe grec aborde cinq types de solides différents, qui sont le tétraèdre, l’hexaèdre (ou cube), l’octaèdre, le dodécaèdre et l’icosaèdre, qui ont respectivement quatre, six, huit, douze et vingt faces.
Platon associe ses solides aux quatre éléments de base. Le tétraèdre, par exemple, représentait le feu, en raison de ses pointes et de ses arêtes vives, tandis que l’hexaèdre était lié à la terre, en raison de sa régularité quadrangulaire. L’octaèdre et l’icosaèdre, qui sont tous deux composés de triangles, représentent respectivement l’air et l’eau. Enfin, le dodécaèdre a été attribué par Platon aux cieux, car ses douze faces pentagonales correspondent aux douze constellations. Ainsi, à partir de ces cinq solides, Platon a créé une théorie de l’univers.
Les solides de Platon se trouvent également dans les Éléments d’Euclide, bien que, contrairement à Platon, le mathématicien semble avoir été moins intéressé par leurs propriétés symboliques. Au lieu de cela, Euclide, dans le dernier livre de ses Éléments, décrit les solides mathématiquement, et prouve qu’il existe exactement cinq solides réguliers. L’utilisation des cinq solides par Platon pour expliquer l’univers a été plus ou moins abandonnée au cours des siècles suivants, et n’a été reprise qu’au 16ème siècle par l’astronome allemand Johannes Kepler . Depuis lors, les solides de Platon ont fait leur chemin dans la géométrie sacrée, et ont acquis une valeur symbolique supplémentaire. Par exemple, les solides ont été associés au concept hindou des chakras, les nœuds d’énergie psychique dans le corps. L’hexaèdre, par exemple, a été associé au chakra de la racine, l’octaèdre au chakra du cœur, et l’icosaèdre au chakra sacré.
Les solides platoniques ont été ravivés au cours du 16ème siècle par l’astronome allemand Jogannes Kepler, dans son Harmonices Mundi. ( Johannes Kepler / Domaine public )
Pour conclure, la géométrie sacrée a été un moyen important d’expliquer le monde qui nous entoure. La géométrie sacrée a été utilisée par diverses cultures tout au long de l’histoire et continue à être appliquée à l’ère moderne. Les partisans de la géométrie sacrée croient que cette branche des mathématiques détient la clé pour percer les secrets de l’univers. À l’inverse, les critiques ont fait valoir que les données peuvent être adaptées pour correspondre aux théories. En d’autres termes, il est possible pour les partisans de la géométrie sacrée d’appliquer leurs croyances à n’importe quoi.
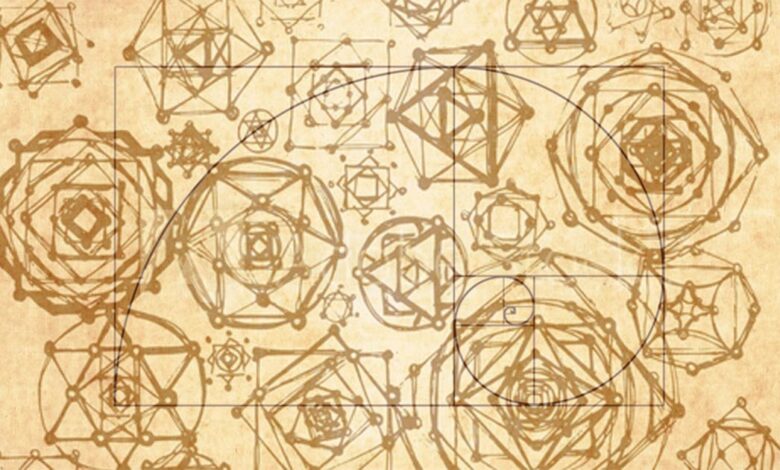
Image du haut : La géométrie sacrée déduit que certaines formes et proportions géométriques contiennent une signification sacrée. L’application de la géométrie sacrée se retrouve dans de nombreuses civilisations à travers le monde. Source : ekaart / Adobe Stock / Spirale de la géométrie sacrée ( lightaspect / Adobe Stock)
Par Wu Mingren
Références
Beyer, C., 2019. Les formes géométriques et leurs significations symboliques. Disponible à l’adresse suivante : https://www.learnreligions.com/geometric-shapes-4086370
Calter, P., 1998. Polygones, carrelages et géométrie sacrée. Disponible à l’adresse : http://www.dartmouth.edu/~matc/math5.geometry/unit5/unit5.html
Cambridge University Press, 2020. géométrie. Disponible à l’adresse suivante : https://dictionary.cambridge.org/dictionary/english/geometry
Carlson, R., 2012. La signification de la géométrie sacrée. Disponible à l’adresse suivante : https://sacredgeometryinternational.com/the-meaning-of-sacred-geometry
Carlson, S. C., 2019. Ratio d’or. Disponible à l’adresse suivante : https://www.britannica.com/science/golden-ratio
Dafoe, S. A., 2007. Tetractys. Disponible à l’adresse suivante : http://www.masonicdictionary.com/tetractys.html
Devlin, K., 2007. Le mythe qui ne disparaîtra pas. Disponible à l’adresse suivante : https://www.maa.org/external_archive/devlin/devlin_05_07.html
Helibron, J. L., 2013. Solide platonique. Disponible à l’adresse suivante : https://www.britannica.com/science/Platonic-solid
Helibron, J. L., 2020. Géométrie. Disponible à l’adresse suivante : https://www.britannica.com/science/geometry
Mann, A., 2019. Phi : Le Golden Ratio. Disponible à l’adresse suivante : https://www.livescience.com/37704-phi-golden-ratio.html
O’Connor, J. J. & Robertson, E. F., 1999. Euclide d’Alexandrie. Disponible à l’adresse suivante : https://mathshistory.st-andrews.ac.uk/Biographies/Euclid/
Rawles, B., 2020. Tutoriel d’introduction à la géométrie sacrée. Disponible à l’adresse suivante : https://www.geometrycode.com/sacred-geometry/
Sage Goddess, Inc. 2020. Qu’est-ce que la géométrie sacrée ? Disponible à l’adresse suivante : https://www.sagegoddess.com/what-is-sacred-geometry/
Snider, A. C., 2018. Le pouvoir mystique de la géométrie sacrée. Disponible à l’adresse : https://medium.com/@AmberCSnider/the-mystical-power-of-sacred-geometry-9…
van der Waerden, B. L., 2019. Euclide. Disponible à l’adresse suivante : https://www.britannica.com/biography/Euclid-Greek-mathematician
www.ancient-symbols.com, 2020. Le symbole des tétractys. Disponible à l’adresse suivante : https://www.ancient-symbols.com/symbols-directory/tetractys.html
www.crystalinks.com, 2020. Géométrie sacrée. Disponible à l’adresse suivante : https://www.crystalinks.com/sg.html
www.ms.uky.edu, 2011. Les origines de la géométrie. Disponible sur : http://www.ms.uky.edu/~droyster/courses/fall11/MA341/Classnotes/Chapter%2001-The%20Origins%20of%20Geometry.pdf
.
