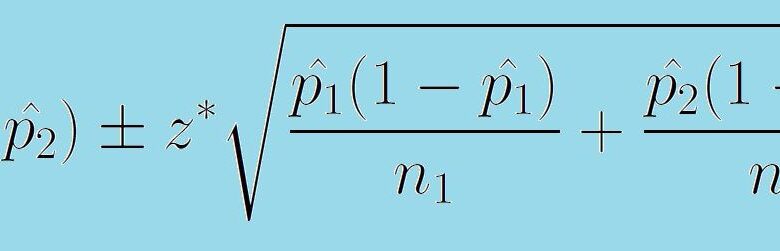
Contents
Les intervalles de confiance sont une partie des statistiques inférentielles. L’idée de base de ce sujet est d’estimer la valeur d’un paramètre inconnu de la population en utilisant un échantillon statistique. Nous pouvons non seulement estimer la valeur d’un paramètre, mais nous pouvons également adapter nos méthodes pour estimer la différence entre deux paramètres liés. Par exemple, nous pouvons vouloir trouver la différence entre le pourcentage de la population américaine masculine votant en faveur d’un texte de loi particulier et la population féminine votant.
Nous verrons comment faire ce type de calcul en construisant un intervalle de confiance pour la différence entre deux proportions de la population. Ce faisant, nous examinerons une partie de la théorie qui sous-tend ce calcul. Nous verrons certaines similitudes dans la manière de construire un intervalle de confiance pour une seule proportion de la population ainsi qu’un intervalle de confiance pour la différence de deux moyennes de la population.
Généralités
Avant d’examiner la formule spécifique que nous utiliserons, considérons le cadre général dans lequel s’inscrit ce type d’intervalle de confiance. La forme du type d’intervalle de confiance que nous allons examiner est donnée par la formule suivante :
Estimation +/- Marge d’erreur
De nombreux intervalles de confiance sont de ce type. Il y a deux nombres que nous devons calculer. La première de ces valeurs est l’estimation du paramètre. La deuxième valeur est la marge d’erreur. Cette marge d’erreur tient compte du fait que nous disposons d’une estimation. L’intervalle de confiance nous fournit une gamme de valeurs possibles pour notre paramètre inconnu.
Conditions
Nous devons nous assurer que toutes les conditions sont remplies avant de faire un calcul. Pour trouver un intervalle de confiance pour la différence entre deux proportions de population, nous devons nous assurer que les conditions suivantes sont remplies :
- Nous disposons de deux échantillons aléatoires simples provenant de grandes populations. Ici, « grand » signifie que la population est au moins 20 fois plus grande que la taille de l’échantillon. Les tailles des échantillons seront désignées par n1 et n2.
- Nos individus ont été choisis indépendamment les uns des autres.
- Il y a au moins dix succès et dix échecs dans chacun de nos échantillons.
Si le dernier point de la liste n’est pas satisfait, il peut y avoir un moyen de contourner ce problème. Nous pouvons modifier la construction de l’intervalle de confiance plus quatre et obtenir des résultats robustes. À mesure que nous avançons, nous supposons que toutes les conditions ci-dessus ont été remplies.
Échantillons et proportions de la population
Nous sommes maintenant prêts à construire notre intervalle de confiance. Nous commençons par l’estimation de la différence entre nos proportions de population. Ces deux proportions de la population sont estimées par une proportion de l’échantillon. Ces proportions d’échantillon sont des statistiques que l’on obtient en divisant le nombre de succès dans chaque échantillon, puis en divisant par la taille de l’échantillon respectif.
La première proportion de la population est désignée par p1. Si le nombre de succès dans notre échantillon de cette population est k1, alors nous avons une proportion d’échantillon de k1 / n1.
Nous indiquons cette statistique par p̂1. Nous lisons ce symbole comme « p1-hat » parce qu’il ressemble au symbole p1 avec un chapeau sur le dessus.
De la même manière, nous pouvons calculer une proportion d’échantillon à partir de notre deuxième population. Le paramètre de cette population est p2. Si le nombre de succès dans notre échantillon de cette population est k2, et que notre proportion d’échantillon est p̂2 = k2 / n2.
Ces deux statistiques deviennent la première partie de notre intervalle de confiance. L’estimation de p1 est p̂1. L’estimation de p2 est p̂2. L’estimation de la différence p1 – p2 est donc p̂1 – p̂2.
Distribution de la différence des proportions de l’échantillon
Ensuite, nous devons obtenir la formule de la marge d’erreur. Pour ce faire, nous allons d’abord examiner la distribution de l’échantillon de p̂1 . Il s’agit d’une distribution binomiale avec une probabilité de succès des essais p1 et n1. La moyenne de cette distribution est la proportion p1. L’écart-type de ce type de variable aléatoire a une variance de p1 (1 – p1 )/n1.
La distribution de l’échantillon de p̂2 est similaire à celle de p̂1 . Il suffit de changer tous les indices de 1 à 2 pour obtenir une distribution binomiale avec une moyenne de p2 et une variance de p2 (1 – p2 )/n2.
Nous avons maintenant besoin de quelques résultats de statistiques mathématiques afin de déterminer la répartition de l’échantillon de p̂1 – p̂2. La moyenne de cette distribution est de p1 – p2. En raison du fait que les variances s’additionnent, nous voyons que la variance de la distribution d’échantillonnage est p1 (1 – p1 )/n1 + p2 (1 – p2 )/n2. L’écart-type de la distribution est la racine carrée de cette formule.
Nous devons procéder à quelques ajustements. Le premier est que la formule de l’écart-type de p̂1 – p̂2 utilise les paramètres inconnus de p1 et p2. Bien sûr, si nous connaissions vraiment ces valeurs, alors ce ne serait pas du tout un problème statistique intéressant. Nous n’aurions pas besoin d’estimer la différence entre p1 et p2.. Au lieu de cela, nous pourrions simplement calculer la différence exacte.
Ce problème peut être résolu en calculant une erreur type plutôt qu’un écart type. Il suffit de remplacer les proportions de la population par des proportions de l’échantillon. Les erreurs standard sont calculées à partir de statistiques plutôt que de paramètres. Une erreur standard est utile car elle permet d’estimer efficacement un écart-type. Cela signifie pour nous qu’il n’est plus nécessaire de connaître la valeur des paramètres p1 et p2… Comme ces proportions d’échantillon sont connues, l’erreur standard est donnée par la racine carrée de l’expression suivante
p̂1 (1 – p̂1 )/n1 + p̂2 (1 – p̂2 )/n2.
Le deuxième point que nous devons aborder est la forme particulière de notre distribution d’échantillons. Il s’avère que nous pouvons utiliser une distribution normale pour approximer la distribution d’échantillonnage de p̂1 – p̂2. La raison en est quelque peu technique, mais elle est exposée dans le paragraphe suivant.
Les sites p̂1 et p̂2 ont tous deux une distribution d’échantillonnage binomiale. Chacune de ces distributions binomiales peut être assez bien approchée par une distribution normale. Ainsi, p̂1 – p̂2 est une variable aléatoire. Elle est formée comme une combinaison linéaire de deux variables aléatoires. Chacune d’entre elles est approchée par une distribution normale. Par conséquent, la distribution d’échantillonnage de p̂1 – p̂2 est également une distribution normale.
Formule de l’intervalle de confiance
Nous avons maintenant tout ce dont nous avons besoin pour assembler notre intervalle de confiance. L’estimation est (p̂1 – p̂2) et la marge d’erreur est de z* [ p̂1 (1 – p̂1 )/n1 + p̂2 (1 – p̂2 )/n2.]0.5. La valeur que nous entrons pour z* est dictée par le niveau de confiance C. Les valeurs couramment utilisées pour z* sont 1,645 pour une confiance de 90% et 1,96 pour une confiance de 95%. Ces valeurs pour z* désignent la partie de la distribution normale standard où exactement C pour cent de la distribution se situe entre -z* et z*.
La formule suivante nous donne un intervalle de confiance pour la différence entre deux proportions de la population :
(p̂1 – p̂2) +/- z* [ p̂1 (1 – p̂1 )/n1 + p̂2 (1 – p̂2 )/n2.]0.5