Introduction à la fonction Delta de Dirac

La fonction delta de Dirac est le nom donné à une structure mathématique destinée à représenter un objet ponctuel idéalisé, tel qu’une masse ou une charge ponctuelle. Elle a de larges applications dans la mécanique quantique et le reste de la physique quantique, car elle est généralement utilisée dans la fonction d’onde quantique. La fonction delta est représentée par le symbole grec en minuscules delta, écrit comme une fonction : δ(x).

Comment fonctionne la fonction Delta

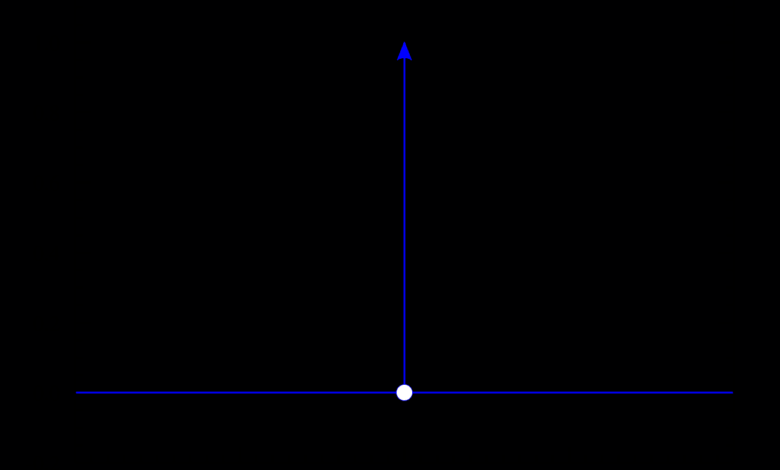
Cette représentation est obtenue en définissant la fonction delta de Dirac de manière à ce qu’elle ait une valeur de 0 partout sauf à la valeur d’entrée de 0. Elle représente alors un pic qui est infiniment élevé. L’intégrale prise sur toute la ligne est égale à 1. Si vous avez étudié le calcul, vous avez probablement déjà rencontré ce phénomène. Gardez à l’esprit qu’il s’agit d’un concept qui est normalement présenté aux étudiants après des années d’études universitaires en physique théorique.

En d’autres termes, les résultats sont les suivants pour la fonction delta la plus élémentaire δ(x), avec une variable unidimensionnelle x, pour certaines valeurs d’entrée aléatoires :

• δ(5) = 0
• δ(-20) = 0
• δ(38.4) = 0
• δ(-12.2) = 0
• δ(0.11) = 0
• δ(0) = ∞

Vous pouvez augmenter l’échelle de la fonction en la multipliant par une constante. Selon les règles de calcul, la multiplication par une valeur constante augmentera également la valeur de l’intégrale par ce facteur constant. Puisque l’intégrale de δ(x) sur tous les nombres réels est 1, sa multiplication par une constante de donnerait une nouvelle intégrale égale à cette constante. Ainsi, par exemple, 27δ(x) a une intégrale sur tous les nombres réels de 27.

Un autre élément utile à prendre en compte est que, puisque la fonction a une valeur non nulle uniquement pour une entrée de 0, alors si vous regardez une grille de coordonnées où votre point n’est pas aligné sur 0, cela peut être représenté par une expression à l’intérieur de l’entrée de la fonction. Ainsi, si vous voulez représenter l’idée que la particule est à une position x = 5, alors vous écrirez la fonction delta de Dirac comme suit : δ(x – 5) = ∞ [since δ(5 – 5) = ∞].

Si vous voulez ensuite utiliser cette fonction pour représenter une série de particules ponctuelles dans un système quantique, vous pouvez le faire en additionnant diverses fonctions delta de dirac. Pour un exemple concret, une fonction avec des points à x = 5 et x = 8 pourrait être représentée par δ(x – 5) + δ(x – 8). Si vous preniez ensuite une intégrale de cette fonction sur tous les nombres, vous obtiendriez une intégrale qui représente les nombres réels, même si les fonctions sont 0 à tous les endroits autres que les deux où il y a des points. Ce concept peut ensuite être étendu pour représenter un espace à deux ou trois dimensions (au lieu du cas unidimensionnel que j’ai utilisé dans mes exemples).

Il s’agit d’une brève introduction à un sujet très complexe. La chose essentielle à réaliser est que la fonction delta de Dirac existe fondamentalement dans le seul but de donner un sens à l’intégration de la fonction. Lorsque l’intégration n’a pas lieu, la présence de la fonction delta de Dirac n’est pas particulièrement utile. Mais en physique, lorsqu’il s’agit de passer d’une région sans particules qui n’existent soudainement qu’à un seul point, c’est très utile.

Source de la fonction Delta

Dans son livre de 1930, Principles of Quantum Mechanics, le physicien théoricien anglais Paul Dirac a exposé les éléments clés de la mécanique quantique, y compris la notation bra-ket et aussi sa fonction delta de Dirac. Ces concepts sont devenus la norme dans le domaine de la mécanique quantique au sein de l’équation de Schrodinger.