La théorie de la relativité d’Einstein

La théorie de la relativité d’Einstein est une théorie célèbre, mais elle est peu comprise. La théorie de la relativité fait référence à deux éléments différents de la même théorie : la relativité générale et la relativité spéciale. La théorie de la relativité spéciale a été introduite la première et a été considérée plus tard comme un cas particulier de la théorie plus complète de la relativité générale.

La relativité générale est une théorie de la gravitation qu’Albert Einstein a développée entre 1907 et 1915, avec des contributions de beaucoup d’autres après 1915.

Théorie des concepts de la relativité

La théorie de la relativité d’Einstein inclut l’interfonctionnement de plusieurs concepts différents, dont

• La théorie de la relativité spéciale d’Einstein – le comportement localisé des objets dans les cadres de référence inertiels, qui n’est généralement pertinent qu’à des vitesses très proches de la vitesse de la lumière
• Transformations de Lorentz – les équations de transformation utilisées pour calculer les changements de coordonnées dans le cadre de la relativité spéciale
• La théorie de la relativité générale d’Einstein – la théorie plus complète, qui traite la gravité comme un phénomène géométrique d’un système de coordonnées spatio-temporelles courbes, qui comprend également des cadres de référence non inertiels (c’est-à-dire accélérateurs)
• Principes fondamentaux de la relativité

Relativité

La relativité classique (définie initialement par Galileo Galilei et affinée par Sir Isaac Newton) implique une simple transformation entre un objet en mouvement et un observateur dans un autre cadre de référence inertiel. Si vous marchez dans un train en mouvement, et que quelqu’un qui est stationné au sol vous observe, votre vitesse par rapport à l’observateur sera la somme de votre vitesse par rapport au train et de la vitesse du train par rapport à l’observateur. Vous êtes dans un cadre de référence inertiel, le train lui-même (et toute personne assise dessus) est dans un autre, et l’observateur est dans un autre encore.

Le problème est que l’on croyait, dans la majorité des années 1800, que la lumière se propageait comme une onde à travers une substance universelle connue sous le nom d’éther, qui aurait compté comme un cadre de référence distinct (semblable au train dans l’exemple ci-dessus). La célèbre expérience de Michelson-Morley, cependant, n’avait pas réussi à détecter le mouvement de la Terre par rapport à l’éther et personne ne pouvait expliquer pourquoi. Quelque chose clochait avec l’interprétation classique de la relativité appliquée à la lumière… et le domaine était donc mûr pour une nouvelle interprétation quand Einstein est arrivé.

Introduction à la relativité spéciale

En 1905, Albert Einstein a publié (entre autres) un article intitulé « On the Electrodynamics of Moving Bodies » dans la revue Annalen der Physik. L’article présentait la théorie de la relativité spéciale, basée sur deux postulats :

Les postulats d’Einstein

Principe de la relativité (premier postulat): Les lois de la physique sont les mêmes pour tous les référentiels inertiels.

Principe de la constance de la vitesse de la lumière (deuxième postulat): La lumière se propage toujours dans le vide (c’est-à-dire dans un espace vide ou « espace libre ») à une vitesse définie, c, qui est indépendante de l’état de mouvement du corps émetteur.

En fait, l’article présente une formulation plus formelle et mathématique des postulats. La formulation des postulats est légèrement différente de celle d’un manuel scolaire en raison de problèmes de traduction, de l’allemand mathématique à l’anglais compréhensible.

Le deuxième postulat est souvent écrit à tort pour inclure que la vitesse de la lumière dans le vide est c dans tous les cadres de référence. Il s’agit en fait d’un résultat dérivé des deux postulats, plutôt que d’une partie du second postulat lui-même.

Le premier postulat est à peu près le bon sens. Le second postulat, en revanche, est celui de la révolution. Einstein avait déjà introduit la théorie des photons de la lumière dans son article sur l’effet photoélectrique (qui rendait l’éther inutile). Le second postulat était donc la conséquence de photons sans masse se déplaçant à la vitesse c dans le vide. L’éther n’avait plus de rôle particulier en tant que cadre de référence inertiel « absolu », il était donc non seulement inutile mais aussi qualitativement inutilisable dans le cadre de la relativité spéciale.

Quant au papier lui-même, l’objectif était de réconcilier les équations de Maxwell pour l’électricité et le magnétisme avec le mouvement des électrons à une vitesse proche de celle de la lumière. Le résultat de l’article d’Einstein a été d’introduire de nouvelles transformations de coordonnées, appelées transformations de Lorentz, entre les cadres de référence inertiels. À faible vitesse, ces transformations étaient essentiellement identiques au modèle classique, mais à grande vitesse, près de la vitesse de la lumière, elles donnaient des résultats radicalement différents.

Les effets de la relativité spéciale

La relativité spéciale entraîne plusieurs conséquences de l’application des transformations de Lorentz à des vitesses élevées (proches de la vitesse de la lumière). Parmi celles-ci, on peut citer

• La dilatation du temps (y compris le populaire « paradoxe des jumeaux »)
• Contraction de la longueur
• Transformation de la vitesse
• Addition de vitesse relativiste
• L’effet Doppler relativiste
• Simultanéité et synchronisation de l’horloge
• Une dynamique relativiste
• L’énergie cinétique relativiste
• Masse relativiste
• Énergie totale relativiste

En outre, de simples manipulations algébriques des concepts ci-dessus donnent deux résultats significatifs qui méritent d’être mentionnés individuellement.

Relation masse-énergie

Einstein a pu montrer que la masse et l’énergie étaient liées, grâce à la célèbre formule E=mc2. Cette relation a été prouvée de la manière la plus spectaculaire au monde lorsque des bombes nucléaires ont libéré l’énergie de masse à Hiroshima et Nagasaki à la fin de la Seconde Guerre mondiale.

La vitesse de la lumière

Aucun objet ayant une masse ne peut accélérer jusqu’à la vitesse de la lumière. Un objet sans masse, comme un photon, peut se déplacer à la vitesse de la lumière. (Un photon n’accélère pas réellement, cependant, puisqu’il se déplace toujours exactement à la vitesse de la lumière).

Mais pour un objet physique, la vitesse de la lumière est une limite. L’énergie cinétique à la vitesse de la lumière va jusqu’à l’infini, elle ne peut donc jamais être atteinte par accélération.

Certains ont fait remarquer qu’un objet pourrait en théorie se déplacer à une vitesse supérieure à celle de la lumière, tant qu’il n’accélère pas pour atteindre cette vitesse. Jusqu’à présent, aucune entité physique n’a cependant jamais affiché cette propriété.

Adopter une relativité particulière

En 1908, Max Planck a appliqué le terme « théorie de la relativité » pour décrire ces concepts, en raison du rôle clé que la relativité y jouait. À l’époque, bien sûr, le terme s’appliquait uniquement à la relativité spéciale, car il n’y avait pas encore de relativité générale.

La relativité d’Einstein n’a pas été immédiatement adoptée par l’ensemble des physiciens parce qu’elle semblait si théorique et contre-intuitive. Lorsqu’il a reçu son prix Nobel en 1921, c’était spécifiquement pour sa solution à l’effet photoélectrique et pour ses « contributions à la physique théorique ». La relativité était encore trop controversée pour qu’on y fasse spécifiquement référence.

Au fil du temps, cependant, les prévisions de la relativité spéciale se sont avérées exactes. Par exemple, il a été démontré que les horloges qui volent autour du monde ralentissent de la durée prévue par la théorie.

Les origines des transformations de Lorentz

Albert Einstein n’a pas créé les transformations de coordonnées nécessaires à la relativité spéciale. Il n’a pas eu à le faire parce que les transformations de Lorentz dont il avait besoin existaient déjà. Einstein était passé maître dans l’art de prendre des travaux antérieurs et de les adapter à de nouvelles situations, et il l’a fait avec les transformations de Lorentz tout comme il avait utilisé la solution de Planck de 1900 à la catastrophe ultraviolette du rayonnement des corps noirs pour élaborer sa solution à l’effet photoélectrique, et ainsi développer la théorie des photons de la lumière.

Les transformations ont en fait été publiées pour la première fois par Joseph Larmor en 1897. Une version légèrement différente avait été publiée une décennie plus tôt par Woldemar Voigt, mais sa version comportait un carré dans l’équation de dilatation temporelle. Néanmoins, les deux versions de l’équation se sont révélées invariantes sous l’équation de Maxwell.

Le mathématicien et physicien Hendrik Antoon Lorentz a cependant proposé l’idée d’un « temps local » pour expliquer la simultanéité relative en 1895, et a commencé à travailler indépendamment sur des transformations similaires pour expliquer le résultat nul de l’expérience de Michelson-Morley. Il a publié ses transformations de coordonnées en 1899, apparemment sans connaître la publication de Larmor, et a ajouté la dilatation temporelle en 1904.

En 1905, Henri Poincare modifie les formulations algébriques et les attribue à Lorentz sous le nom de « transformations de Lorentz », modifiant ainsi les chances d’immortalité de Larmor à cet égard. La formulation de la transformation de Poincare était, pour l’essentiel, identique à celle qu’utiliserait Einstein.

Les transformations s’appliquaient à un système de coordonnées à quatre dimensions, avec trois coordonnées spatiales (x, y, & z) et une coordonnée unique

x’ = ( x – ut ) / sqrt ( 1 – u2 / c2 )y’ = y

z’ = z

t’ = { t – ( u / c2 ) x } / sqrt ( 1 – u2 / c2 )

Les transformations sont fournies principalement à des fins de démonstration. Leurs applications spécifiques seront traitées séparément. Le terme 1/sqrt (1 – u2/c2) apparaît si fréquemment en relativité qu’il est désigné par le symbole grec gamma dans certaines représentations.

Il convient de noter que dans les cas où u << c, le dénominateur s'effondre essentiellement au sqrt(1), qui est juste 1. Gamma devient juste 1 dans ces cas. De même, le terme u/c2 devient également très petit. Par conséquent, la dilatation de l'espace et du temps est inexistante à un niveau significatif à des vitesses beaucoup plus lentes que la vitesse de la lumière dans le vide.

Conséquences des transformations

La relativité spéciale entraîne plusieurs conséquences de l’application des transformations de Lorentz à des vitesses élevées (proches de la vitesse de la lumière). Parmi celles-ci, on peut citer

• Dilatation du temps (y compris le populaire « Twin Paradox »)
• Contraction de la longueur
• Transformation de la vitesse
• Addition de vitesse relativiste
• L’effet Doppler relativiste
• Simultanéité et synchronisation de l’horloge
• Une dynamique relativiste
• L’énergie cinétique relativiste
• Masse relativiste
• Énergie totale relativiste

La controverse Lorentz & Einstein

Certaines personnes soulignent que la plupart des travaux réels pour la relativité spéciale avaient déjà été réalisés au moment où Einstein les a présentés. Les concepts de dilatation et de simultanéité pour les corps en mouvement étaient déjà en place et les mathématiques avaient déjà été développées par Lorentz & Poincare. Certains vont même jusqu’à qualifier Einstein de plagiaire.

Ces accusations ont une certaine validité. Il est certain que la « révolution » d’Einstein a été construite sur les épaules de beaucoup d’autres travaux, et Einstein a obtenu bien plus de crédit pour son rôle que ceux qui ont fait le travail de base.

En même temps, il faut considérer qu’Einstein a pris ces concepts de base et les a montés sur un cadre théorique qui en faisait non seulement des astuces mathématiques pour sauver une théorie mourante (c’est-à-dire l’éther), mais plutôt des aspects fondamentaux de la nature à part entière. Il n’est pas clair que Larmor, Lorentz ou Poincaré aient eu l’intention de faire un geste aussi audacieux, et l’histoire a récompensé Einstein pour cette perspicacité et cette audace.

Évolution de la relativité générale

Dans la théorie d’Albert Einstein de 1905 (relativité spéciale), il a montré que parmi les cadres de référence inertiels, il n’y avait pas de cadre « préféré ». Le développement de la relativité générale est en partie dû à une tentative de montrer que cela était également vrai pour les cadres de référence non inertiels (c’est-à-dire accélérateurs).

En 1907, Einstein publie son premier article sur les effets gravitationnels de la lumière dans le cadre de la relativité spéciale. Dans cet article, Einstein expose son « principe d’équivalence », selon lequel l’observation d’une expérience sur la Terre (avec une accélération gravitationnelle g) serait identique à l’observation d’une expérience dans une fusée qui se déplace à une vitesse g. Le principe d’équivalence peut être formulé comme suit

nous […] supposent l’équivalence physique complète d’un champ gravitationnel et une accélération correspondante du système de référence.

comme l’a dit Einstein ou, alternativement, comme le présente un livre de physique moderne :

Aucune expérience locale ne permet de distinguer les effets d’un champ gravitationnel uniforme dans un cadre inertiel non accélérateur et les effets d’un cadre de référence (non inertiel) à accélération uniforme.

Un deuxième article sur le sujet est paru en 1911, et en 1912, Einstein travaillait activement à la conception d’une théorie générale de la relativité qui expliquerait la relativité spéciale, mais aussi la gravitation en tant que phénomène géométrique.

En 1915, Einstein a publié un ensemble d’équations différentielles connues sous le nom d’équations de champ d’Einstein. La relativité générale d’Einstein décrivait l’univers comme un système géométrique à trois dimensions spatiales et une dimension temporelle. La présence de la masse, de l’énergie et du moment (collectivement quantifiés en tant que densité masse-énergie ou tension-énergie) a entraîné la courbure de ce système de coordonnées spatio-temporelles. La gravité se déplaçait donc le long de la route la plus « simple » ou la moins énergique le long de cette courbe espace-temps.

Les mathématiques de la relativité générale

Dans les termes les plus simples possibles, et en faisant abstraction des mathématiques complexes, Einstein a trouvé la relation suivante entre la courbure de l’espace-temps et la densité de masse énergétique :

(courbure de l’espace-temps) = (densité de masse-énergie) * 8 pi G / c4

L’équation montre une proportion directe et constante. La constante gravitationnelle, G, provient de la loi de Newton sur la gravité, tandis que la dépendance à la vitesse de la lumière, c, est attendue de la théorie de la relativité spéciale. Dans le cas d’une densité masse-énergie nulle (ou proche de zéro) (c’est-à-dire un espace vide), l’espace-temps est plat. La gravitation classique est un cas spécial de manifestation de la gravité dans un champ gravitationnel relativement faible, où le terme c4 (un très grand dénominateur) et G (un très petit numérateur) rendent la correction de courbure faible.

Encore une fois, Einstein n’a pas sorti ça d’un chapeau. Il a beaucoup travaillé avec la géométrie riemannienne (une géométrie non euclidienne développée par le mathématicien Bernhard Riemann des années plus tôt), bien que l’espace résultant soit un multiple lorentzien en 4 dimensions plutôt qu’une géométrie strictement riemannienne. Néanmoins, les travaux de Riemann étaient essentiels pour que les équations du champ d’Einstein soient complètes.

Moyenne de la relativité générale

Pour faire une analogie avec la relativité générale, considérez que vous avez tendu un drap de lit ou un morceau d’élastique à plat, en attachant fermement les coins à certains poteaux sécurisés. Vous commencez alors à placer sur le drap des objets de poids divers. Si vous placez quelque chose de très léger, le drap se courbera un peu vers le bas sous le poids de celui-ci. Mais si vous placez quelque chose de lourd, la courbure sera encore plus grande.

Supposons qu’un objet lourd soit posé sur la feuille et que vous placiez un second objet, plus léger, sur la feuille. La courbure créée par l’objet plus lourd fera « glisser » l’objet plus léger le long de la courbe vers lui, en essayant d’atteindre un point d’équilibre où il ne bougera plus. (Dans ce cas, bien sûr, il y a d’autres considérations : une bille roulera plus loin qu’un cube ne glisserait, en raison des effets de frottement et autres).

Cela est similaire à la façon dont la relativité générale explique la gravité. La courbure d’un objet léger n’affecte pas beaucoup l’objet lourd, mais la courbure créée par l’objet lourd est ce qui nous empêche de flotter dans l’espace. La courbure créée par la Terre maintient la lune en orbite, mais en même temps, la courbure créée par la lune est suffisante pour affecter les marées.

Prouver la relativité générale

Tous les résultats de la relativité spéciale soutiennent également la relativité générale, puisque les théories sont cohérentes. La relativité générale explique également tous les phénomènes de la mécanique classique, car eux aussi sont cohérents. En outre, plusieurs résultats confirment les prédictions uniques de la relativité générale :

• Précession du périhélie de Mercure
• Déviation gravitationnelle de la lumière des étoiles
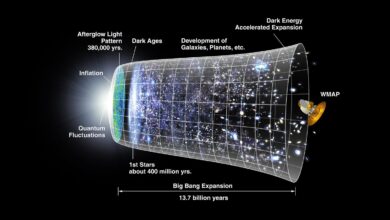
• Expansion universelle (sous la forme d’une constante cosmologique)
• Retard des échos radar
• Radiation des trous noirs

Principes fondamentaux de la relativité

• Principe général de la relativité : Les lois de la physique doivent être identiques pour tous les observateurs, qu’elles soient accélérées ou non.
• Principe de la covariance générale : Les lois de la physique doivent prendre la même forme dans tous les systèmes de coordonnées.
• Le mouvement inertiel est un mouvement géodésique : Les lignes mondiales de particules non affectées par des forces (c’est-à-dire le mouvement inertiel) sont des géodésiques temporelles ou nulles de l’espace-temps. (Cela signifie que le vecteur tangent est soit négatif, soit nul).
• Invariance Lorentz locale : Les règles de la relativité spéciale s’appliquent localement pour tous les observateurs inertiels.
• Courbure spatio-temporelle : Comme le décrivent les équations de champ d’Einstein, la courbure de l’espace-temps en réponse à la masse, à l’énergie et à la quantité de mouvement fait que les influences gravitationnelles sont considérées comme une forme de mouvement inertiel.

Le principe d’équivalence, qu’Albert Einstein a utilisé comme point de départ de la relativité générale, s’avère être une conséquence de ces principes.

La relativité générale et la constante cosmologique

En 1922, les scientifiques ont découvert que l’application des équations de champ d’Einstein à la cosmologie a entraîné une expansion de l’univers. Einstein, croyant en un univers statique (et pensant donc que ses équations étaient erronées), a ajouté une constante cosmologique aux équations de champ, ce qui a permis d’obtenir des solutions statiques.

Edwin Hubble, en 1929, a découvert qu’il y avait un décalage vers le rouge des étoiles lointaines, ce qui impliquait qu’elles se déplaçaient par rapport à la Terre. L’univers, semblait-il, était en expansion. Einstein a supprimé la constante cosmologique de ses équations, la qualifiant de la plus grande bévue de sa carrière.

Dans les années 1990, l’intérêt pour la constante cosmologique est revenu sous la forme d’une énergie sombre. Les solutions apportées aux théories quantiques des champs ont abouti à la présence d’une énorme quantité d’énergie dans le vide quantique de l’espace, ce qui a entraîné une expansion accélérée de l’univers.

Relativité générale et mécanique quantique

Lorsque les physiciens tentent d’appliquer la théorie quantique des champs au champ gravitationnel, les choses se compliquent. En termes mathématiques, les quantités physiques impliquées divergent, ou se traduisent par l’infini. Les champs gravitationnels dans le cadre de la relativité générale nécessitent un nombre infini de constantes de correction, ou « renormalisation », pour les adapter en équations résolvables.

Les tentatives pour résoudre ce « problème de renormalisation » sont au cœur des théories de la gravité quantique. Les théories de la gravité quantique fonctionnent généralement à l’envers, en prédisant une théorie puis en la testant plutôt qu’en essayant de déterminer les constantes infinies nécessaires. C’est un vieux truc de la physique, mais jusqu’à présent, aucune des théories n’a été suffisamment prouvée.

Autres controverses assorties

Le problème majeur de la relativité générale, qui a par ailleurs connu un grand succès, est son incompatibilité globale avec la mécanique quantique. Une grande partie de la physique théorique est consacrée à essayer de concilier les deux concepts : l’un qui prédit des phénomènes macroscopiques dans l’espace et l’autre qui prédit des phénomènes microscopiques, souvent dans des espaces plus petits qu’un atome.

En outre, la notion même d’espace-temps d’Einstein suscite quelques inquiétudes. Qu’est-ce que l’espace-temps ? Existe-t-il physiquement ? Certains ont prédit une « mousse quantique » qui se répandrait dans l’univers. De récentes tentatives de théorie des cordes (et ses filiales) utilisent cette représentation quantique de l’espace-temps ou d’autres. Un article récent du magazine New Scientist prédit que l’espace-temps pourrait être un superfluide quantique et que l’univers entier pourrait tourner sur un axe.

Certaines personnes ont fait remarquer que si l’espace-temps existe en tant que substance physique, il agirait comme un cadre de référence universel, tout comme l’éther l’avait fait. Les anti-relativistes sont ravis de cette perspective, tandis que d’autres y voient une tentative non scientifique de discréditer Einstein en ressuscitant un concept mort depuis un siècle.

Certaines questions relatives aux singularités des trous noirs, où la courbure de l’espace-temps s’approche de l’infini, ont également fait douter que la relativité générale représente correctement l’univers. Il est cependant difficile d’en être sûr, car les trous noirs ne peuvent être étudiés que de loin à l’heure actuelle.

Dans l’état actuel des choses, la relativité générale connaît un tel succès qu’il est difficile d’imaginer que ces incohérences et controverses lui porteront un grand préjudice, jusqu’à ce qu’un phénomène contredisant les prédictions mêmes de la théorie se présente.