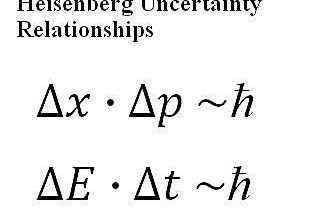
Contents
L’effet photoélectrique a posé un défi important à l’étude de l’optique dans la dernière partie du XIXe siècle. Il a remis en question la théorie classique des ondes de la lumière, qui était la théorie dominante de l’époque. C’est la solution à ce dilemme de la physique qui a catapulté Einstein sur le devant de la scène dans la communauté des physiciens, lui valant finalement le prix Nobel en 1921.
Qu’est-ce que l’effet photoélectrique ?
Annalen der Physik
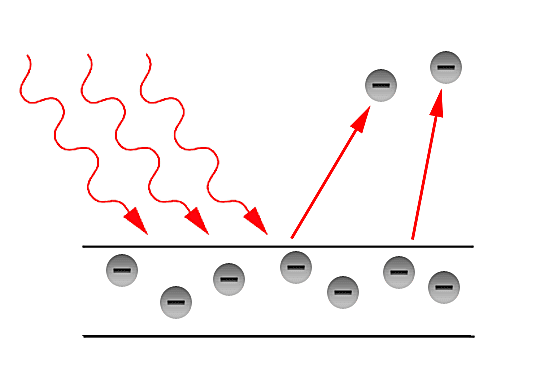
Lorsqu’une source de lumière (ou, plus généralement, un rayonnement électromagnétique) est incidente sur une surface métallique, celle-ci peut émettre des électrons. Les électrons émis de cette manière sont appelés photoélectrons (bien qu’ils ne soient encore que des électrons). Ceci est représenté sur l’image de droite.
Mise en place de l’effet photoélectrique
En administrant un potentiel de tension négative (la boîte noire sur la photo) au collecteur, il faut plus d’énergie aux électrons pour compléter le voyage et initier le courant. Le point auquel aucun électron n’atteint le collecteur est appelé potentiel d’arrêt Vs et peut être utilisé pour déterminer l’énergie cinétique maximale Kmax des électrons (qui ont une charge électronique e) en utilisant l’équation suivante :
Kmax = eVs
L’explication de la vague classique
Iwork function phiPhi
Trois prédictions principales découlent de cette explication classique :
- L’intensité du rayonnement doit avoir une relation proportionnelle avec l’énergie cinétique maximale qui en résulte.
- L’effet photoélectrique devrait se produire pour toute lumière, quelle que soit sa fréquence ou sa longueur d’onde.
- Il devrait y avoir un délai de l’ordre de quelques secondes entre le contact du rayonnement avec le métal et la libération initiale des photoélectrons.
Le résultat expérimental
- L’intensité de la source lumineuse n’a pas eu d’effet sur l’énergie cinétique maximale des photoélectrons.
- En dessous d’une certaine fréquence, l’effet photoélectrique ne se produit pas du tout.
- Il n’y a pas de délai significatif (moins de 10-9 s) entre l’activation de la source lumineuse et l’émission des premiers photoélectrons.
Comme vous pouvez le constater, ces trois résultats sont à l’opposé des prévisions de la théorie des vagues. Non seulement cela, mais ils sont tous les trois complètement contre-intuitifs. Pourquoi la lumière à basse fréquence ne déclencherait-elle pas l’effet photoélectrique, puisqu’elle transporte toujours de l’énergie ? Comment les photoélectrons se libèrent-ils si rapidement ? Et, ce qui est peut-être le plus curieux, pourquoi l’ajout d’une plus grande intensité n’entraîne-t-il pas une libération plus énergique des électrons ? Pourquoi la théorie des ondes échoue-t-elle si complètement dans ce cas alors qu’elle fonctionne si bien dans de nombreuses autres situations
La merveilleuse année d’Einstein
Albert Einstein Annalen der Physik
S’appuyant sur la théorie du rayonnement du corps noir de Max Planck, Einstein a proposé que l’énergie du rayonnement ne soit pas distribuée de manière continue sur le front d’onde, mais qu’elle soit plutôt localisée en petits faisceaux (appelés plus tard photons). L’énergie du photon serait associée à sa fréquence (ν), par une constante de proportionnalité connue sous le nom de constante de Planck (h), ou alternativement, en utilisant la longueur d’onde (λ) et la vitesse de la lumière (c) :
E = hν = hc / λ
ou l’équation du momentum : p = h / λ
νφ
Si, toutefois, il y a un excès d’énergie, au-delà de φ, dans le photon, l’énergie excédentaire est convertie en énergie cinétique de l’électron :
Kmax = hν – φ
L’énergie cinétique maximale est obtenue lorsque les électrons les moins liés se libèrent, mais qu’en est-il des plus liés ? Ceux dans lesquels il y a juste assez d’énergie dans le photon pour le faire se détacher, mais l’énergie cinétique qui en résulte est nulle ? En réglant Kmax à zéro pour cette fréquence de coupure (νc), on obtient :
νc = φ / h
ou la longueur d’onde de coupure : λc = hc / φ
Après Einstein
Plus important encore, l’effet photoélectrique, et la théorie des photons qu’il a inspirée, a écrasé la théorie classique des ondes de la lumière. Bien que personne ne puisse nier que la lumière se comportait comme une onde, après le premier article d’Einstein, il était indéniable qu’elle était aussi une particule.