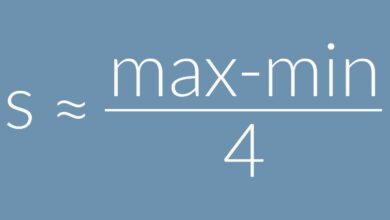Contents
Il existe de nombreuses mains nommées différentes au poker. Une main facile à expliquer s’appelle une couleur. Ce type de main consiste à ce que chaque carte ait la même couleur.
Certaines des techniques de combinatoire, ou l’étude du comptage, peuvent être appliquées pour calculer les probabilités de tirer certains types de mains au poker. La probabilité de recevoir une couleur est relativement simple à trouver, mais elle est plus compliquée que le calcul de la probabilité de recevoir une couleur royale.
Hypothèses
Par souci de simplicité, nous supposerons que cinq cartes sont distribuées à partir d’un jeu de 52 cartes standard sans remplacement. Aucune carte n’est un joker, et le joueur conserve toutes les cartes qui lui sont distribuées.
Nous ne nous préoccuperons pas de l’ordre dans lequel ces cartes sont tirées, chaque main est donc une combinaison de cinq cartes tirées d’un jeu de 52 cartes. Il y a un nombre total de C(52, 5) = 2.598.960 mains distinctes possibles. Cet ensemble de mains constitue notre espace d’échantillonnage.
Probabilité de chasse d’eau directe
Nous commençons par trouver la probabilité d’une quinte flush. Une quinte flush est une main avec les cinq cartes en ordre séquentiel, qui sont toutes de la même couleur. Afin de calculer correctement la probabilité d’une quinte flush, il y a quelques stipulations que nous devons faire.
Nous ne comptons pas une quinte flush royale comme une quinte flush. Ainsi, la quinte flush la plus élevée consiste en un neuf, un dix, un valet, une reine et un roi de la même couleur. Comme un as peut compter une carte basse ou haute, la quinte flush la plus basse est un as, deux, trois, quatre et cinq de la même couleur. Les quintes ne peuvent pas passer par l’as, donc la dame, le roi, l’as, le deux et le trois ne sont pas comptés comme une quinte.
Ces conditions signifient qu’il y a neuf quintes d’un même costume. Comme il y a quatre couleurs différentes, cela fait 4 x 9 = 36 quintes au total. La probabilité d’une quinte flush est donc de 36/2 598 960 = 0,0014 %. Cela équivaut approximativement à 1/72193. Donc, à long terme, on s’attendrait à voir cette main une fois sur 72 193.
Probabilité de chasse d’eau
Une couleur est composée de cinq cartes de la même couleur. Il ne faut pas oublier qu’il y a quatre couleurs avec un total de 13 cartes chacune. Un flush est donc une combinaison de cinq cartes d’un total de 13 de la même couleur. Cela se fait en C(13, 5) = 1287 façons. Comme il y a quatre couleurs différentes, il y a un total de 4 x 1287 = 5148 couleurs possibles.
Certaines de ces quintes ont déjà été comptées comme des mains de rang supérieur. Nous devons soustraire le nombre de quintes et de quintes royales de 5148 afin d’obtenir des quintes qui ne sont pas de rang supérieur. Il y a 36 quintes flush et 4 quintes royales. Nous devons nous assurer de ne pas compter deux fois ces mains. Cela signifie qu’il y a 5148 – 40 = 5108 quintes qui ne sont pas d’un rang supérieur.
Nous pouvons maintenant calculer la probabilité d’une chasse d’eau comme suit : 5108/2 598 960 = 0,1965%. Cette probabilité est d’environ 1/509. Donc, à long terme, une main sur 509 est une chasse d’eau.
Classements et probabilités
Nous pouvons voir, d’après ce qui précède, que le classement de chaque main correspond à sa probabilité. Plus une main est probable, plus son classement est bas. Plus une main est improbable, plus son classement est élevé.