Contents
La civilisation occidentale a toujours été fascinée par la civilisation qui s’est développée le long du Nil vers 3 000 ans avant Jésus-Christ. Les intellectuels grecs, comme Thalès, ont visité l’Égypte et ont été séduits par la conception et l’exactitude mathématique de la forme des pyramides. Pendant des millénaires, l’Égypte ancienne a été considérée comme synonyme de sagesse par les civilisations du bassin méditerranéen, mais surtout par l’Occident.
Un texte qui révèle un exemple de cette sagesse est le papyrus du Rhin, un document qui semble être un abécédaire des mathématiques, autrement banal. Mais une grande partie de ce que les érudits savent des mathématiques égyptiennes provient de ce texte.
Découverte et utilisation du papyrus du Rhin
Le papyrus du Rhin est un document datant d’environ 1 650 avant J.-C. Il a été trouvé et acheté par Alexander Henry Rhind en 1858 dans une ville du Nil en Égypte. Le texte du papyrus se trouve actuellement au British Museum.
Lorsqu’il a été examiné pour la première fois par des universitaires, il s’est avéré être un document mathématique. Il a été écrit par un scribe du nom d’Ahmes et consiste en une série de problèmes de pratique pour les scribes novices.
Les problèmes mathématiques révèlent des informations importantes sur la façon dont les anciens Egyptiens travaillaient avec les multiplications, les divisions et les fractions. Comme le nom de son auteur original est connu, le papyrus Rhin est aussi parfois appelé papyrus Ahmès.
Contexte historique des mathématiques égyptiennes
L’Égypte ancienne a été l’une des premières civilisations relativement avancées et centralisées à émerger dans la région méditerranéenne antique, et probablement dans le monde entier. Elle trouve son origine dans les communautés agricoles qui ont émergé le long du Nil. La plus grande partie de l’Égypte est un désert, mais le Nil offre une longue et étroite bande de terre arable.
Le Nil coule à travers des collines calcaires dans une plaine inondable. Il finit par se jeter dans le delta du Nil qui se jette dans la mer Méditerranée. Les inondations régulières le long du Nil rendent les terres autour du fleuve particulièrement fertiles pour la culture. La fertilité du sol est l’une des principales raisons pour lesquelles l’Égypte était destinée à devenir un centre de civilisation avec l’essor de l’agriculture.
Il y a de nombreuses raisons pour lesquelles les anciens Egyptiens avaient besoin d’apprendre les mathématiques. L’une d’entre elles était liée à l’agriculture et aux saisons. Comme les agriculteurs égyptiens dépendaient des crues régulières du Nil, il était utile de savoir quand les inondations se produiraient afin que les agriculteurs puissent se préparer. Pour cette raison, les anciens Egyptiens se sont enseignés l’astronomie.
Les prêtres égyptiens ont finalement compris que la saison des inondations était annoncée par la montée héliaque de l’étoile Sirius. C’est pourquoi les Égyptiens ont été très attentifs à observer le mouvement de Sirius. Les prêtres égyptiens ont finalement utilisé ces calculs pour créer le calendrier égyptien .
Une section du calendrier hiéroglyphique du temple de Kom Ombo, montrant la transition du mois XII au mois I. (Ad Meskens / CC BY-SA 3.0 )
Une autre raison pour laquelle les mathématiques étaient importantes pour l’Égypte, et les civilisations anciennes en général, était le maintien d’une société complexe. Le gouvernement égyptien de l’Antiquité avait besoin de garder une trace des impôts et du commerce et il s’appuyait sur une classe de scribes professionnels.
Ces scribes, en plus d’apprendre à lire et à écrire, devaient également apprendre les mathématiques. La plupart de ce que l’on sait sur la façon dont les Égyptiens faisaient des mathématiques est révélé dans le papyrus rhénan et dans des documents similaires.
Les mathématiques égyptiennes révélées dans le papyrus du Rhin
Les anciens Egyptiens ne semblent pas avoir pensé de manière abstraite aux chiffres. Par exemple, si vous mentionniez le chiffre 7 à une ancienne Égyptienne, elle penserait probablement d’abord à un regroupement de 7 objets plutôt qu’au concept du chiffre 7. Pour les anciens Egyptiens, les nombres étaient des quantités d’objets physiques plutôt que des abstractions qui existaient séparément des objets qu’ils décrivaient.
Néanmoins, les anciens Egyptiens étaient très habiles dans l’utilisation de l’arithmétique pour accomplir des tâches de comptabilité et d’ingénierie. Les chiffres égyptiens, comme les chiffres romains, sont étroitement liés au système d’écriture égyptien.
Chiffres égyptiens tels qu’on les trouve dans le papyrus du Rhin. ( Drutska / Adobe Stock )
Les hiéroglyphes égyptiens ont probablement évolué à partir d’images utilisées pour représenter des mots ou des idées. Avec le temps, ils ont évolué en symboles représentant les sons des mots.
Les hiéroglyphes sont constitués de symboles qui représentent à la fois des mots et des sons de mots. Par exemple, le mot « croyance » en anglais pourrait être représenté par l’image d’une abeille et l’image d’une feuille, formant ainsi la feuille d’abeille qui, bien sûr, fait résonner le mot « croyance ».
Les hiéroglyphes sont utilisés de cette manière afin que les symboles représentant les sons des mots puissent être utilisés pour épeler des phrases entières. Les symboles hiéroglyphiques peuvent également avoir des significations multiples. Par exemple, l’image d’une oreille peut signifier à la fois « oreille » et « son ».
La société égyptienne devenant plus complexe, il fallait enregistrer les recettes fiscales, les transactions commerciales, calculer la quantité de matériaux nécessaires à la construction d’un temple, et d’autres tâches nécessitant des calculs mathématiques. Les symboles hiéroglyphiques en sont venus à représenter également des quantités numériques. Les Égyptiens avaient un système de nombres en base 10.
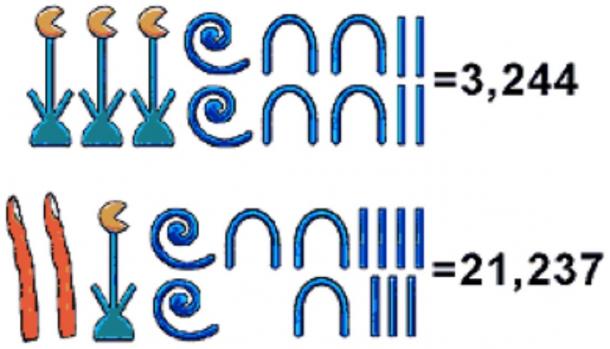
Ils avaient un symbole distinct pour 1, 10, 100, etc. Il existait un système de chiffres bloquants qui était utilisé dans les inscriptions sur les monuments en pierre et dans les documents officiels. Un ensemble de chiffres abrégés plus commode était également utilisé par les scribes lors de la rédaction de documents sur papyri.
Par rapport aux chiffres arabes, qui sont utilisés dans la plupart des pays du monde aujourd’hui pour effectuer des opérations mathématiques, le système de chiffres égyptien a des limites quant aux problèmes mathématiques qui peuvent être facilement résolus à l’aide de ce système. Par exemple, il est difficile de représenter ou de travailler avec de très grands nombres en utilisant les chiffres égyptiens.
La valeur numérique la plus élevée représentée par un seul chiffre égyptien est 1 million. Si un mathématicien voulait représenter 1 milliard en utilisant des chiffres égyptiens, ce serait très lourd et ennuyeux puisqu’il devrait écrire le symbole 1 million mille fois ou inventer un nouveau symbole. Cela pourrait fonctionner au début, mais que se passerait-il s’il fallait représenter un trillion ou un quadrillion ?
En mathématiques égyptiennes, les multiples de ces valeurs étaient exprimés en répétant le symbole autant de fois que nécessaire. (BbcNkl / CC BY-SA 4.0 )
Le calcul de très grands nombres n’est pas pratique en utilisant les chiffres égyptiens car les très grands nombres sont difficiles à représenter, et un nouveau symbole doit être inventé chaque fois que les valeurs numériques deviennent trop grandes pour être représentées de manière pratique en utilisant les symboles actuels. Ainsi, le système de chiffres égyptiens est moins flexible qu’un système comme le système de chiffres arabes dans lequel les dix mêmes symboles peuvent être utilisés pour représenter un nombre de n’importe quelle taille.
Il aurait également été difficile de faire de l’algèbre en utilisant les chiffres égyptiens. Les chiffres égyptiens manquent de symboles spécifiques pour l’infini ou les nombres négatifs, par exemple. La raison de ces limitations dans les chiffres égyptiens est probablement que les anciens scribes égyptiens n’avaient pas besoin de travailler avec des nombres négatifs, l’infini ou de très grands nombres.
Les scribes égyptiens s’occupaient principalement de résoudre des problèmes mathématiques dans les transactions commerciales, la comptabilité et les projets d’ingénierie qui n’exigent pas nécessairement des mathématiques plus avancées que la géométrie et l’arithmétique. Les anciens Égyptiens auraient eu du mal à traiter des nombres supérieurs à un million, mais ils n’en avaient généralement pas besoin, car il était probablement rare qu’ils rencontrent des nombres aussi importants dans leur travail habituel. Les anciens Égyptiens étaient également ingénieux dans la conception de méthodes de multiplication, de division, de fractions et d’autres opérations mathématiques qui n’impliquaient que des additions et des soustractions pour lesquelles les chiffres égyptiens sont faciles à utiliser.
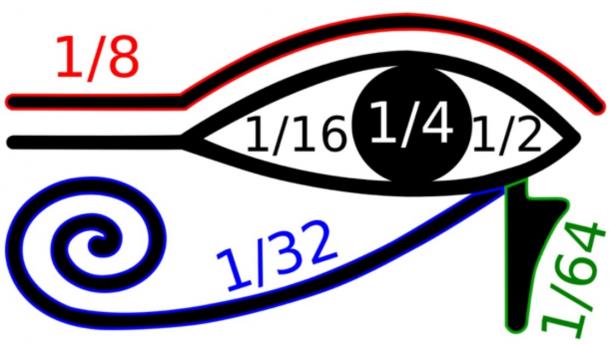
On pense que des parties isolées du symbole de l' »œil d’Horus » étaient utilisées pour écrire diverses fractions. (BenduKiwi / CC BY-SA 3.0 )
Comme d’autres cultures, les anciens Egyptiens avaient leurs propres traditions et méthodes pour résoudre les problèmes mathématiques qui ne correspondent pas nécessairement à celles utilisées dans l’Occident moderne. L’addition et la soustraction sont simples et directes dans les mathématiques égyptiennes.
Ils consistent simplement à ajouter ou à retirer des chiffres de différentes valeurs numériques jusqu’à ce qu’un nombre soit atteint. Si un scribe voulait ajouter 20 à 76 pour obtenir 96, il n’aurait qu’à ajouter les symboles appropriés.
L’approche égyptienne de la multiplication et de la division consiste à faire un tableau de multiples et à l’utiliser pour effectuer une série d’opérations d’addition et de soustraction. Par exemple, pour multiplier 15 par 45, on fait un tableau avec une série de nombres qui sont successivement doublés en commençant par 1 dans une colonne.
Le doublement successif se poursuit jusqu’à ce que le chiffre de 15 soit atteint. La deuxième colonne est constituée de multiples de 45 correspondant aux chiffres de la première colonne. Ceci est illustré dans le tableau ci-dessous.
Depuis 16 > 15, il suffit d’aller jusqu’à 8 dans la colonne 1. Les valeurs de la colonne 2 seront des multiples de 45 multipliés par les entrées correspondantes de la colonne 1. Une fois le tableau réalisé, les nombres de la Colonne 1 qui totalisent 15 sont marqués.
Dans ce cas, 1+ 2 + 4 + 8 = 15. Comme toutes les entrées de la colonne 1 sont nécessaires pour obtenir une somme de 15, toutes les entrées de la colonne 2 sont additionnées. 45 + 90 + 180 + 360 = 675. Ainsi, 15 fois 45 est égal à 675. La division est la même, mais à l’inverse.
Problème de mathématiques égyptien du papyrus du Rhin. (Bakha~commonswiki / Domaine public )
Les fractions étaient importantes dans le monde antique pour les transactions commerciales. Dans l’Égypte ancienne, les fractions étaient également représentées différemment de ce qu’elles sont aujourd’hui. Par exemple, 2/5 s’écrivait 1/3 + 1/15. Les fractions devaient aussi toujours être représentées sous forme de parties d’unités ou de fractions avec un numérateur de 1.
Les mathématiques et la vision du monde de l’Égypte ancienne
Bien que les anciens Egyptiens soient connus pour leurs impressionnants exploits en matière d’ingénierie et de calculs astronomiques utilisant des calculs mathématiques, les Egyptiens n’ont pas apporté grand chose au domaine des mathématiques lui-même. Ils n’étaient pas nécessairement beaucoup plus avancés que les civilisations environnantes en termes de connaissances mathématiques.
Les Égyptiens ont créé des calendriers, construit des pyramides et des temples, et géré l’une des premières et des plus durables civilisations de l’histoire en utilisant principalement l’arithmétique et la géométrie de base. Rien ne prouve qu’ils aient fait beaucoup pour trouver des concepts ou des idées sur les mathématiques qui étaient inconnus des autres civilisations à l’époque.
Les Égyptiens utilisaient des relations numériques spéciales telles que le nombre d’or. Cependant, il n’y a guère de preuves que les anciens scribes égyptiens aient reconnu leur importance.
Les anciens Egyptiens ont simplement trouvé que ces ratios étaient utiles pour construire des monuments. Il y a peu de preuves qu’ils se souciaient ou reconnaissaient les implications théoriques du nombre d’or.
Papyrus du Rhin montrant les mathématiques égyptiennes. (Luestling~commonswiki / Domaine public )
Bien qu’il soit possible qu’il y ait eu des équivalents égyptiens natifs de Thalès et d’Euclide, le dossier historique implique que la culture égyptienne semble avoir été plus concernée par les applications pratiques des mathématiques que par les concepts théoriques en mathématiques. Les sciences et les mathématiques étaient destinées à des activités pratiques telles que l’ingénierie, la comptabilité et la fabrication de calendriers.
Cette attitude envers les mathématiques peut indiquer une différence importante entre la façon dont les anciens Égyptiens et la plupart des anciennes cultures voyaient le monde et la façon dont certains des philosophes grecs présocratiques de l’autre côté de la Méditerranée commençaient à voir le monde au VIe siècle avant J.-C.
Les anciens Egyptiens, comme d’autres civilisations anciennes, expliquaient le monde par la mythologie. La mythologie diffère de la science en ce sens qu’elle recherche les relations et la téléologie pour expliquer le monde.
La mythologie ne s’intéresse pas à l’éclat du soleil ni à sa composition. La mythologie s’interroge sur le but ultime du soleil et sur sa signification pour l’humanité et les dieux.
Carte stellaire de l’Empire du Milieu égyptien. (NebMaatRa / Licence publique générale GNU)
Une vision scientifique du monde, en revanche, s’intéresse davantage à la description et aux processus. Les chiffres ne vous disent généralement pas ce qui motive les dieux à envoyer de la pluie pour que les cultures puissent pousser.
Ils n’expliquent pas non plus la motivation du dieu soleil qui traverse le ciel pour apporter la lumière au monde, mais ils décrivent comment le soleil se déplace et les conditions atmosphériques nécessaires à la pluie. Les chiffres n’expliquent pas la signification et le but, mais ils décrivent des processus et des mécanismes.
La science demande : « Qu’est-ce que l’univers et comment fonctionne-t-il ? La mythologie demande : « Pourquoi y a-t-il un univers et que signifie-t-il pour moi, ma famille, ma communauté, mon peuple et mes dieux ?
Si certains philosophes de la Grèce antique s’intéressaient tant aux chiffres, c’est peut-être en partie parce qu’ils s’intéressaient à la description du monde physique et des processus qui le régissent. Ils commençaient à avoir une vision scientifique ou proto-scientifique du monde.
Les anciens Egyptiens, en revanche, avaient une vision du monde essentiellement mythologique. Les chiffres décrivaient le monde, mais pas la partie du monde qui les intéressait le plus.
Pour adapter une citation attribuée à Galileo Galilei, les anciens Egyptiens posaient la question « Comment allez-vous au ciel ? Les philosophes grecs pré-socratiques, qui ont visité l’Égypte, se demandaient « Comment vont les cieux ?
Directement ou indirectement, les anciens Egyptiens ont eu une influence significative sur la civilisation occidentale et islamique. C’est pourquoi une grande partie du monde moderne est redevable aux anciens Égyptiens et à leurs scribes qui ont pu construire les pyramides et diriger les économies impériales avec moins de connaissances mathématiques qu’un collégien moderne.
Image du haut : Le papyrus mathématique du Rhin. Source : The British Museum / CC BY-NC-SA 4.0 .
Par Caleb Strom
Références
Bellis, M. 2019. Citations de Galileo Galilei . ThoughtCo. [Online] Disponible à l’adresse suivante : https://www.thoughtco.com/galileo-galilei-quotes-1992011
Dickinson, D. 2013. L’astronomie des jours de chien de l’été . L’univers aujourd’hui . [Online] Disponible à l’adresse suivante : https://www.universetoday.com/103894/the-astronomy-of-the-dog-days-of-summer/
Gray, J., Berggren, J., Folkerts, M., Knorr, W. et Fraser, C. 2019. Les mathématiques dans l’Égypte ancienne . Encyclopaedia Britannica. [Online] Disponible à l’adresse suivante : https://www.britannica.com/science/mathematics/Mathematics-in-ancient-Egypt
Ecrivains et éditeurs de l’Encyclopédie du Nouveau Monde. 2018. Mythologie. Encyclopédie du Nouveau Monde. [Online] Disponible à l’adresse suivante : https://www.newworldencyclopedia.org/entry/Mythology
O’Connor, J., et Robertson, E. 2000. Un aperçu des mathématiques égyptiennes . École de mathématiques et de statistiques de l’université de Saint Andrews, Écosse. [Online] Disponible à l’adresse suivante : http://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_mathematics.html
O’Connor, J., et Robertson, E. 2000. Chiffres égyptiens . École de mathématiques et de statistiques de l’université de Saint Andrews, Écosse. [Online] Disponible à l’adresse suivante : http://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html
O’Connor, J., et Robertson, E. 2000. Les mathématiques dans le papyrus égyptien . École de mathématiques et de statistiques de l’université de Saint Andrews, Écosse. [Online] Disponible à l’adresse suivante : http://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_papyri.html
Les rédacteurs de l’Encyclopaedia Britannica. 2008. Papyrus du Rhin . Encyclopaedia Britannica. [Online] Disponible à l’adresse suivante : https://www.britannica.com/topic/Rhind-papyrus
Walton, J. 2010. Le monde perdu de la première genèse : débat sur la cosmologie ancienne et les origines . InterVarsity Press.
Wente, E., Samuel, A., Dorman, P., Bowman, A., et Baines, J. 2019. L’Égypte ancienne . Encyclopaedia Britannica. [Online] Disponible à l’adresse suivante : https://www.britannica.com/place/ancient-Egypt#ref22284
.