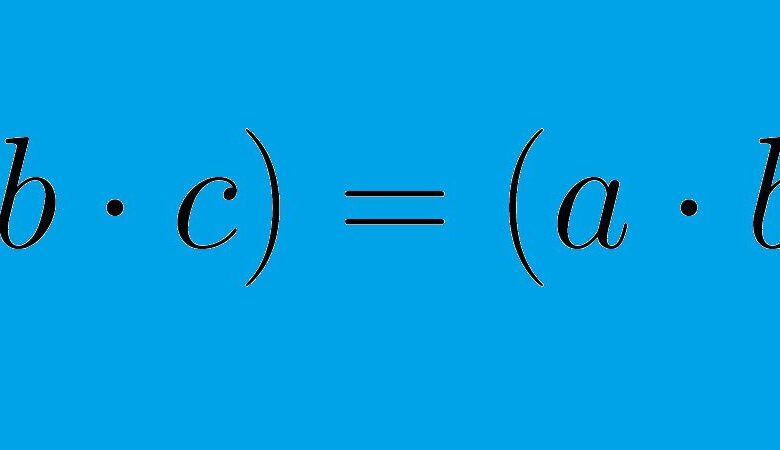
Contents
Plusieurs propriétés mathématiques sont utilisées en statistique et en probabilité ; deux d’entre elles, les propriétés commutatives et associatives, sont généralement associées à l’arithmétique de base des nombres entiers, rationnels et réels, bien qu’elles apparaissent également dans les mathématiques plus avancées.
Ces propriétés – commutatives et associatives – sont très similaires et peuvent être facilement confondues. C’est pourquoi il est important de comprendre la différence entre les deux.
La propriété commutative concerne l’ordre de certaines opérations mathématiques. Pour une opération binaire – qui n’implique que deux éléments – cela peut être démontré par l’équation a + b = b + a. L’opération est commutative parce que l’ordre des éléments n’affecte pas le résultat de l’opération. La propriété associative, en revanche, concerne le regroupement des éléments dans une opération. Cela peut être démontré par l’équation (a + b) + c = a + (b + c). Le regroupement des éléments, comme indiqué par les parenthèses, n’affecte pas le résultat de l’équation. Notez que lorsque la propriété commutative est utilisée, les éléments d’une équation sont réarrangés. Lorsque la propriété associative est utilisée, les éléments sont simplement regroupés.
Propriété commutative
En termes simples, la propriété commutative indique que les facteurs d’une équation peuvent être réarrangés librement sans affecter le résultat de l’équation. La propriété commutative concerne donc l’ordonnancement des opérations, y compris l’addition et la multiplication des nombres réels, des entiers et des nombres rationnels.
Par exemple, les nombres 2, 3 et 5 peuvent être additionnés dans n’importe quel ordre sans affecter le résultat final :
2 + 3 + 5 = 10
3 + 2 + 5 = 10
5 + 3 + 2 = 10
De même, les chiffres peuvent être multipliés dans n’importe quel ordre sans affecter le résultat final :
2 x 3 x 5 = 30
3 x 2 x 5 = 30
5 x 3 x 2 = 30
La soustraction et la division, cependant, ne sont pas des opérations qui peuvent être commutatives car l’ordre des opérations est important. Les trois nombres ci-dessus ne peuvent pas, par exemple, être soustraits dans n’importe quel ordre sans affecter la valeur finale :
2 – 3 – 5 = -6
3 – 5 – 2 = -4
5 – 3 – 2 = 0
En conséquence, la propriété commutative peut être exprimée par les équations a + b = b + a et a x b = b x a. Quel que soit l’ordre des valeurs dans ces équations, les résultats seront toujours les mêmes.
Propriété associative
La propriété associative indique que le regroupement des facteurs dans une opération peut être modifié sans affecter le résultat de l’équation. Cela peut être exprimé par l’équation a + (b + c) = (a + b) + c. Quelle que soit la paire de valeurs ajoutée en premier dans l’équation, le résultat sera le même.
Par exemple, prenez l’équation 2 + 3 + 5. Quelle que soit la façon dont les valeurs sont regroupées, le résultat de l’équation sera 10 :
(2 + 3) + 5 = (5) + 5 = 10
2 + (3 + 5) = 2 + (8) = 10
Comme pour la propriété commutative, les exemples d’opérations qui sont associatives comprennent l’addition et la multiplication de nombres réels, d’entiers et de nombres rationnels. Toutefois, contrairement à la propriété commutative, la propriété associative peut également s’appliquer à la multiplication de matrices et à la composition de fonctions.
Comme les équations de propriété commutatives, les équations de propriété associatives ne peuvent pas contenir la soustraction de nombres réels. Prenez, par exemple, le problème arithmétique (6 – 3) – 2 = 3 – 2 = 1 ; si nous changeons le groupement des parenthèses, nous avons 6 – (3 – 2) = 6 – 1 = 5, ce qui change le résultat final de l’équation.
Quelle est la différence ?
Nous pouvons faire la différence entre la propriété associative et la propriété commutative en posant la question suivante : « Changeons-nous l’ordre des éléments, ou changeons-nous le regroupement des éléments ? Si les éléments sont réordonnés, alors la propriété commutative s’applique. Si les éléments sont seulement regroupés, alors la propriété associative s’applique.
Notez toutefois que la seule présence de parenthèses ne signifie pas nécessairement que la propriété associative s’applique. Par exemple :
(2 + 3) + 4 = 4 + (2 + 3)
Cette équation est un exemple de la propriété commutative de l’addition des nombres réels. Cependant, si l’on prête attention à l’équation, on constate que seul l’ordre des éléments a été modifié, et non le regroupement. Pour que la propriété associative s’applique, il faudrait également réorganiser le regroupement des éléments :
(2 + 3) + 4 = (4 + 2) + 3