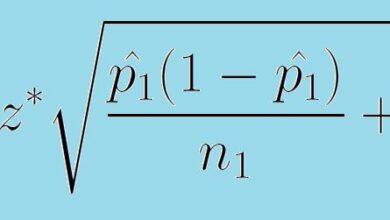Contents
Dans le jeu Monopoly, il y a beaucoup de caractéristiques qui impliquent un certain aspect de probabilité. Bien sûr, comme la méthode de déplacement sur le plateau de jeu consiste à lancer deux dés, il est clair qu’il y a un élément de chance dans le jeu. L’un des endroits où cela est évident est la partie du jeu connue sous le nom de « prison ». Nous allons calculer deux probabilités concernant la prison dans le jeu de Monopoly.
Description de la prison
La prison au Monopoly est un espace dans lequel les joueurs peuvent « juste visiter » en faisant le tour du plateau, ou dans lequel ils doivent aller si quelques conditions sont remplies. En prison, un joueur peut toujours percevoir des loyers et développer des propriétés, mais il ne peut pas se déplacer sur le plateau de jeu. C’est un inconvénient important au début du jeu, lorsque les propriétés ne sont pas possédées. Au fur et à mesure que le jeu progresse, il est parfois plus avantageux de rester en prison, car cela réduit le risque d’atterrir sur les propriétés développées de vos adversaires.
Un joueur peut se retrouver en prison de trois façons.
- On peut simplement atterrir sur l’espace « Aller en prison » du tableau.
- On peut tirer une carte Chance ou Community Chest marquée « Go to Jail ».
- On peut lancer des doubles (les deux chiffres sur les dés sont les mêmes) trois fois de suite.
Il existe également trois façons pour un joueur de sortir de prison
- Utiliser une carte « Sortir de prison ».
- Payer 50
- Le jet double à chacun des trois tours après qu’un joueur soit allé en prison.
Nous examinerons les probabilités du troisième élément de chacune des listes ci-dessus.
Probabilité d’aller en prison
Nous allons d’abord examiner la probabilité d’aller en prison en faisant trois doubles d’affilée. Il y a six résultats différents qui sont des doubles (double 1, double 2, double 3, double 4, double 5 et double 6) sur un total de 36 résultats possibles en lançant deux dés. Ainsi, à chaque tour, la probabilité de lancer un double est de 6/36 = 1/6.
Maintenant, chaque lancer de dés est indépendant. Ainsi, la probabilité qu’un tour donné entraîne le lancement de doubles trois fois de suite est de (1/6) x (1/6) x (1/6) = 1/216. Cela représente environ 0,46 %. Bien que cela puisse sembler un faible pourcentage, étant donné la durée de la plupart des jeux de Monopoly, il est probable que cela arrive à quelqu’un à un moment ou à un autre du jeu.
Probabilité de sortie de prison
Nous passons maintenant à la probabilité de sortir de prison en faisant des doubles. Cette probabilité est un peu plus difficile à calculer car il y a différents cas à prendre en compte :
- La probabilité que nous fassions des doubles au premier lancer est de 1/6.
- La probabilité que nous lancions des doubles au deuxième tour mais pas au premier est (5/6) x (1/6) = 5/36.
- La probabilité que nous lancions des doubles au troisième tour mais pas au premier ni au second est (5/6) x (5/6) x (1/6) = 25/216.
La probabilité de faire rouler des doubles pour sortir de prison est donc de 1/6 + 5/36 + 25/216 = 91/216, soit environ 42%.
Nous pourrions calculer cette probabilité d’une autre manière. Le complément de l’événement « lancer des doubles au moins une fois au cours des trois prochains tours » est « Nous ne lançons pas de doubles du tout au cours des trois prochains tours ». Ainsi, la probabilité de ne pas lancer de doubles est (5/6) x (5/6) x (5/6) = 125/216. Comme nous avons calculé la probabilité du complément de l’événement que nous voulons trouver, nous soustrayons cette probabilité de 100 %. Nous obtenons la même probabilité de 1 – 125/216 = 91/216 que celle que nous avons obtenue par l’autre méthode.
Probabilités des autres méthodes
Les probabilités pour les autres méthodes sont difficiles à calculer. Elles impliquent toutes la probabilité d’atterrir sur un espace particulier (ou d’atterrir sur un espace particulier et de tirer une carte particulière). Trouver la probabilité d’atterrir sur une certaine place en Monopoly est en fait assez difficile. Ce genre de problème peut être résolu par l’utilisation des méthodes de simulation de Monte Carlo.