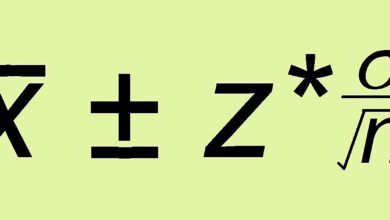Probabilités de croisements dihybrides en génétique

On peut s’étonner que nos gènes et nos probabilités aient des points communs. En raison de la nature aléatoire de la méiose cellulaire, certains aspects de l’étude de la génétique sont en réalité des probabilités appliquées. Nous allons voir comment calculer les probabilités associées aux croisements de dihybrides.

Définitions et hypothèses

Avant de calculer les probabilités, nous définirons les termes que nous utilisons et énoncerons les hypothèses avec lesquelles nous travaillerons.

• Les allèles sont des gènes qui viennent par paires, un de chaque parent. La combinaison de cette paire d’allèles détermine le caractère que présente une progéniture.
• La paire d’allèles est le génotype d’une progéniture. Le trait présenté est le phénotype de la progéniture.
• Les allèles seront considérés comme dominants ou récessifs. Nous supposerons que pour qu’une progéniture présente un trait récessif, il doit y avoir deux copies de l’allèle récessif. Un trait dominant peut se manifester pour un ou deux allèles dominants. Les allèles récessifs seront désignés par une lettre minuscule et les allèles dominants par une lettre majuscule.
• Un individu possédant deux allèles de même type (dominant ou récessif) est dit homozygote. Ainsi, DD et dd sont tous deux homozygotes.
• On dit qu’un individu ayant un allèle dominant et un allèle récessif est hétérozygote. Dd est donc hétérozygote.
• Dans nos croisements dihybrides, nous supposerons que les allèles que nous considérons sont hérités indépendamment les uns des autres.
• Dans tous les exemples, les deux parents sont hétérozygotes pour tous les gènes considérés.

Croix monohybride

Avant de déterminer les probabilités d’un croisement dihybride, nous devons connaître les probabilités d’un croisement monohybride. Supposons que deux parents qui sont hétérozygotes pour un trait produisent une progéniture. Le père a une probabilité de 50% de transmettre l’un ou l’autre de ses deux allèles. De même, la mère a une probabilité de 50 % de transmettre l’un de ses deux allèles.

Nous pouvons utiliser un tableau appelé carré de Punnett pour calculer les probabilités, ou nous pouvons simplement réfléchir aux possibilités. Chaque parent a un génotype Dd, dans lequel chaque allèle a la même probabilité d’être transmis à un descendant. Il y a donc une probabilité de 50% qu’un parent contribue à l’allèle dominant D et une probabilité de 50% que l’allèle récessif d soit contribué. Les possibilités sont résumées :

• Il y a une probabilité de 50% x 50% = 25% que les deux allèles de la progéniture soient dominants.
• Il y a une probabilité de 50% x 50% = 25% que les deux allèles de la progéniture soient récessifs.
• Il y a une probabilité de 50 % x 50 % + 50 % x 50 % = 25 % + 25 % = 50 % que la progéniture soit hétérozygote.

Ainsi, pour les parents qui ont tous deux le génotype Dd, il y a une probabilité de 25% que leur progéniture soit DD, une probabilité de 25% que la progéniture soit dd, et une probabilité de 50% que la progéniture soit Dd. Ces probabilités seront importantes dans ce qui suit.

Croisements et génotypes dihybrides

Nous considérons maintenant une croix dihybride. Cette fois, il existe deux séries d’allèles que les parents peuvent transmettre à leur progéniture. Nous les désignerons par A et a pour l’allèle dominant et récessif du premier ensemble, et B et b pour l’allèle dominant et récessif du second ensemble.

Les deux parents sont hétérozygotes et ont donc le génotype AaBb. Comme ils ont tous deux des gènes dominants, ils auront des phénotypes constitués des traits dominants. Comme nous l’avons dit précédemment, nous ne considérons que les paires d’allèles qui ne sont pas liées entre elles et qui sont héritées indépendamment.

Cette indépendance nous permet d’utiliser la règle de multiplication en probabilité. Nous pouvons considérer chaque paire d’allèles séparément l’un de l’autre. En utilisant les probabilités du croisement monohybride que nous voyons :

• Il y a une probabilité de 50% que la progéniture ait Aa dans son génotype.
• Il y a 25 % de probabilité que la progéniture ait le génotype AA.
• Il y a 25 % de probabilité que la progéniture ait un aa dans son génotype.
• Il y a une probabilité de 50% que la progéniture ait Bb dans son génotype.
• Il y a 25 % de probabilité que la progéniture ait le génotype BB.
• Il y a 25% de probabilité que la progéniture ait bb dans son génotype.

Les trois premiers génotypes sont indépendants des trois derniers de la liste ci-dessus. Nous multiplions donc 3 x 3 = 9 et nous voyons qu’il existe de nombreuses possibilités de combiner les trois premiers avec les trois derniers. C’est la même chose que d’utiliser un diagramme en arbre pour calculer les façons possibles de combiner ces éléments.

Par exemple, puisque Aa a une probabilité de 50% et Bb une probabilité de 50%, il y a une probabilité de 50% x 50% = 25% que la progéniture ait un génotype de AaBb. La liste ci-dessous est une description complète des génotypes possibles, ainsi que de leurs probabilités.

• Le génotype de l’AaBb a une probabilité de 50% x 50% = 25% de se produire.
• Le génotype de l’AaBB a une probabilité de 50% x 25% = 12,5% de se produire.
• Le génotype d’Aabb a une probabilité de 50% x 25% = 12,5% de se produire.
• Le génotype de l’AABb a une probabilité de 25 % x 50 % = 12,5 % d’occurrence.
• Le génotype de l’AABB a une probabilité de 25 % x 25 % = 6,25 % de se produire.
• Le génotype de l’AAbb a une probabilité de 25 % x 25 % = 6,25 % de se produire.
• Le génotype aaBb a une probabilité de 25% x 50% = 12,5% de se produire.
• Le génotype aaBB a une probabilité de 25 % x 25 % = 6,25 % de se produire.
• Le génotype aabb a une probabilité de 25 % x 25 % = 6,25 % de se produire.

Croisements et phénotypes dihybrides

Certains de ces génotypes produiront les mêmes phénotypes. Par exemple, les génotypes de AaBb, AaBB, AABb et AABB sont tous différents les uns des autres, mais ils produiront tous le même phénotype. Tout individu possédant l’un de ces génotypes présentera des traits dominants pour les deux traits considérés.

Nous pouvons alors additionner les probabilités de chacun de ces résultats : 25% + 12,5% + 12,5% + 6,25% = 56,25%. C’est la probabilité que les deux traits soient dominants.

De la même manière, nous pourrions examiner la probabilité que les deux traits soient récessifs. La seule façon d’y parvenir est de disposer du génotype aabb. La probabilité que cela se produise est de 6,25 %.

Nous considérons maintenant la probabilité que la progéniture présente un trait dominant pour A et un trait récessif pour B. Cela peut se produire avec les génotypes de Aabb et AAbb. Nous additionnons les probabilités pour ces génotypes et nous obtenons 18,75%.

Ensuite, nous examinons la probabilité que la progéniture ait un caractère récessif pour A et un caractère dominant pour B. Les génotypes sont aaBB et aaBb. Nous additionnons les probabilités de ces génotypes et nous obtenons une probabilité de 18,75%. Nous aurions également pu faire valoir que ce scénario est symétrique au premier scénario avec un trait dominant pour A et un trait récessif pour B. Par conséquent, la probabilité de ces résultats devrait être identique.

Croix et ratios dihybrides

Une autre façon d’examiner ces résultats est de calculer les ratios que chaque phénotype présente. Nous avons vu les probabilités suivantes :

• 56,25% des deux traits dominants
• 18,75% d’un seul trait dominant
• 6,25% des deux traits récessifs.

Au lieu d’examiner ces probabilités, nous pouvons considérer leurs ratios respectifs. Divisez chacun par 6,25% et nous obtenons les ratios 9:3:1. Lorsque nous considérons qu’il y a deux traits différents à l’étude, les ratios réels sont de 9:3:3:1.

Cela signifie que si nous savons que nous avons deux parents hétérozygotes, si la progéniture présente des phénotypes dont les rapports s’écartent de 9:3:3:1, alors les deux traits que nous considérons ne fonctionnent pas selon l’héritage mendélien classique. Nous devrions plutôt envisager un modèle d’hérédité différent.