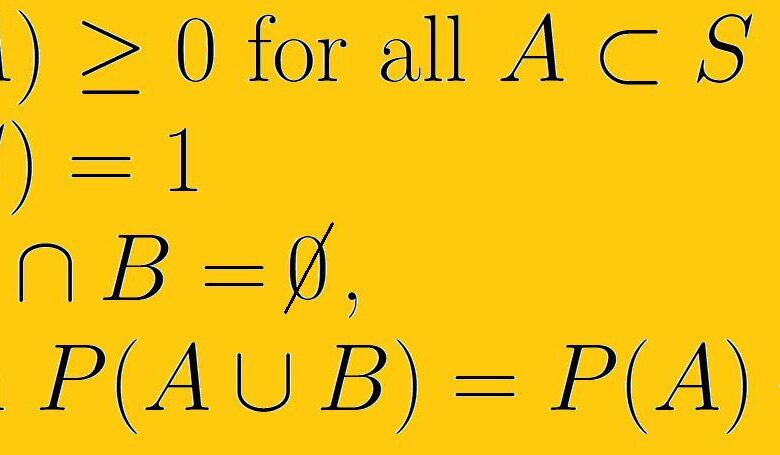
Contents
Une stratégie en mathématiques consiste à commencer par quelques énoncés, puis à en construire d’autres à partir de ces énoncés. Les énoncés de départ sont connus sous le nom d’axiomes. Un axiome est typiquement quelque chose qui est mathématiquement évident. À partir d’une liste relativement courte d’axiomes, la logique déductive est utilisée pour prouver d’autres énoncés, appelés théorèmes ou propositions.
Le domaine des mathématiques connu sous le nom de probabilité n’est pas différent. La probabilité peut être réduite à trois axiomes. C’est le mathématicien Andrei Kolmogorov qui a été le premier à le faire. La poignée d’axiomes qui sous-tendent la probabilité peut être utilisée pour déduire toutes sortes de résultats. Mais quels sont ces axiomes de probabilité ?
Définitions et Préliminaires
Afin de comprendre les axiomes de la probabilité, nous devons d’abord discuter de quelques définitions de base. Nous supposons que nous disposons d’un ensemble de résultats appelé espace d’échantillonnage S. Cet espace d’échantillonnage peut être considéré comme l’ensemble universel pour la situation que nous étudions. L’espace échantillon est composé de sous-ensembles appelés événements E1, E2, …, En.
Nous supposons également qu’il existe un moyen d’attribuer une probabilité à tout événement E. On peut considérer qu’il s’agit d’une fonction qui a un ensemble pour une entrée, et un nombre réel comme une sortie. La probabilité de l’événement E est désignée par P(E).
Axiome 1
Le premier axiome de la probabilité est que la probabilité de tout événement est un nombre réel non négatif. Cela signifie que le plus petit qu’une probabilité puisse jamais être est zéro et qu’elle ne peut pas être infinie. L’ensemble des nombres que nous pouvons utiliser sont des nombres réels. Il s’agit à la fois de nombres rationnels, également appelés fractions, et de nombres irrationnels qui ne peuvent pas être écrits comme des fractions.
Une chose à noter, c’est que cet axiome ne dit rien sur l’importance de la probabilité d’un événement. L’axiome élimine la possibilité de probabilités négatives. Il reflète l’idée que la plus petite probabilité, réservée aux événements impossibles, est égale à zéro.
Axiome deux
Le deuxième axiome de la probabilité est que la probabilité de l’ensemble de l’espace d’échantillonnage est un. Symboliquement, on écrit P(S) = 1. Cet axiome implique la notion que l’espace d’échantillonnage est tout ce qui est possible pour notre expérience de probabilité et qu’il n’y a pas d’événements en dehors de l’espace d’échantillonnage.
En soi, cet axiome ne fixe pas de limite supérieure aux probabilités d’événements qui ne se produisent pas dans tout l’espace de l’échantillon. Il reflète le fait que quelque chose avec une certitude absolue a une probabilité de 100%.
Axe trois
Le troisième axiome de la probabilité traite des événements qui s’excluent mutuellement. Si E1 et E2 sont mutuellement exclusifs, c’est-à-dire qu’ils ont une intersection vide et que nous utilisons U pour désigner l’union, alors P(E1 U E2 ) = P(E1) + P(E2).
L’axiome couvre en fait la situation avec plusieurs événements (même infinis), dont chaque paire est mutuellement exclusive. Tant que cela se produit, la probabilité de l’union des événements est la même que la somme des probabilités :
P(E1 U E2 U … U En ) = P(E1) + P(E2) + … + En
Bien que ce troisième axiome ne semble pas très utile, nous verrons qu’en combinaison avec les deux autres axiomes, il est très puissant.
Applications Axiom
Les trois axiomes fixent une limite supérieure pour la probabilité de tout événement. Nous indiquons le complément de l’événement E par EC. Selon la théorie des ensembles, E et EC ont une intersection vide et sont mutuellement exclusifs. En outre, E U EC = S, l’espace d’échantillonnage entier.
Ces faits, combinés aux axiomes nous donnent :
1 = P(S) = P(E U EC) = P(E) + P(EC) .
Nous réorganisons l’équation ci-dessus et voyons que P(E) = 1 – P(EC). Comme nous savons que les probabilités doivent être non négatives, nous avons maintenant qu’une limite supérieure pour la probabilité de tout événement est 1.
En réorganisant à nouveau la formule, nous avons P(EC) = 1 – P(E). Nous pouvons également déduire de cette formule que la probabilité qu’un événement ne se produise pas est de un moins la probabilité qu’il se produise.
L’équation ci-dessus nous fournit également un moyen de calculer la probabilité de l’événement impossible, dénoté par l’ensemble vide. Pour s’en rendre compte, rappelons que l’ensemble vide est le complément de l’ensemble universel, en l’occurrence SC. Puisque 1 = P(S) + P(SC) = 1 + P(SC), par l’algèbre nous avons P(SC) = 0.
Autres demandes
Ce ne sont là que quelques exemples de propriétés qui peuvent être prouvées directement à partir des axiomes. Il existe beaucoup d’autres résultats en matière de probabilité. Mais tous ces théorèmes sont des extensions logiques des trois axiomes de la probabilité.