Contents
Les premier et troisième quartiles sont des statistiques descriptives qui sont des mesures de la position dans un ensemble de données. Comme la médiane indique le point médian d’un ensemble de données, le premier quartile indique le quart ou le point 25 %. Environ 25 % des valeurs des données sont inférieures ou égales au premier quartile. Le troisième quartile est similaire, mais pour les 25 % supérieurs des valeurs de données. Nous examinerons ces idées plus en détail dans ce qui suit.
La médiane
Il existe plusieurs façons de mesurer le centre d’un ensemble de données. La moyenne, la médiane, le mode et le milieu ont tous leurs avantages et leurs limites pour exprimer le milieu des données. De toutes ces façons de trouver la moyenne, la médiane est la plus résistante aux valeurs aberrantes. Elle marque le milieu des données en ce sens que la moitié des données est inférieure à la médiane.
Le premier quartile
Il n’y a pas de raison que nous nous arrêtions à trouver le juste milieu. Et si nous décidions de poursuivre ce processus ? Nous pourrions calculer la médiane de la moitié inférieure de nos données. Une moitié de 50 % correspond à 25 %. Ainsi, la moitié de la moitié, ou un quart, des données serait en dessous de cette valeur. Comme nous avons affaire à un quart de l’ensemble initial, cette médiane de la moitié inférieure des données est appelée le premier quartile, et est désignée par Q1.
Le troisième quartile
Il n’y a aucune raison pour laquelle nous avons examiné la moitié inférieure des données. Nous aurions plutôt pu examiner la moitié supérieure et effectuer les mêmes opérations que ci-dessus. La médiane de cette moitié, que nous désignerons par Q3, divise également l’ensemble des données en trimestres. Toutefois, ce nombre indique le quart supérieur des données. Ainsi, les trois quarts des données sont en dessous de notre chiffre Q3. C’est pourquoi nous appelons Q3 le troisième quartile.
Un exemple
Pour que tout cela soit clair, prenons un exemple. Il peut être utile de revoir d’abord comment calculer la médiane de certaines données. Commencez par l’ensemble de données suivant :
1, 2, 2, 3, 4, 6, 6, 7, 7, 7, 8, 11, 12, 15, 15, 15, 17, 17, 18, 20
Il y a un total de vingt points de données dans l’ensemble. Nous commençons par trouver la médiane. Comme il y a un nombre pair de valeurs de données, la médiane est la moyenne des dixième et onzième valeurs. En d’autres termes, la médiane est :
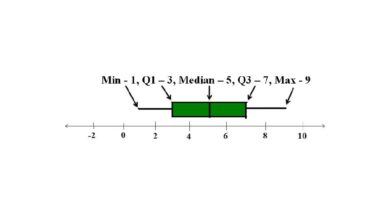
(7 + 8)/2 = 7.5.
Regardez maintenant la moitié inférieure des données. La médiane de cette moitié se trouve entre les cinquième et sixième valeurs de :
1, 2, 2, 3, 4, 6, 6, 7, 7, 7
Ainsi, le premier quartile est égal à Q1 = (4 + 6)/2 = 5
Pour trouver le troisième quartile, regardez la moitié supérieure de l’ensemble de données original. Nous devons trouver la médiane de :
8, 11, 12, 15, 15, 15, 17, 17, 18, 20
Ici, la médiane est (15 + 15)/2 = 15. Ainsi, le troisième quartile Q3 = 15.
Fourchette interquartile et résumé des cinq chiffres
Les quartiles nous aident à avoir une image plus complète de notre ensemble de données. Les premier et troisième quartiles nous donnent des informations sur la structure interne de nos données. La moitié centrale des données se situe entre les premier et troisième quartiles et est centrée sur la médiane. La différence entre les premier et troisième quartiles, appelée intervalle interquartile, montre comment les données sont disposées par rapport à la médiane. Un petit écart interquartile indique que les données sont regroupées autour de la médiane. Un écart interquartile plus important indique que les données sont plus dispersées.
On peut obtenir un tableau plus détaillé des données en connaissant la valeur la plus élevée, appelée valeur maximale, et la valeur la plus basse, appelée valeur minimale. Le minimum, le premier quartile, la médiane, le troisième quartile et le maximum sont un ensemble de cinq valeurs appelées le résumé à cinq chiffres. Un moyen efficace d’afficher ces cinq nombres est appelé boxplot ou graphique en boîtes et moustaches.