Contents
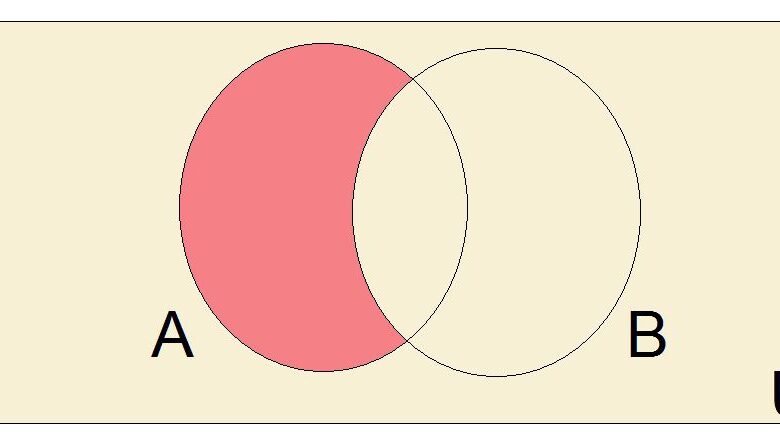
La différence de deux ensembles, écrite A – B, est l’ensemble de tous les éléments de A qui ne sont pas des éléments de B. L’opération de différence, avec l’union et l’intersection, est une opération importante et fondamentale de la théorie des ensembles.
Description de la différence
La soustraction d’un nombre d’un autre peut être pensée de nombreuses manières différentes. Un modèle pour aider à comprendre ce concept est appelé le modèle de soustraction à emporter. Dans ce modèle, le problème 5 – 2 = 3 serait démontré en commençant avec cinq objets, en enlevant deux d’entre eux et en comptant qu’il en reste trois. De la même manière que l’on trouve la différence entre deux nombres, on peut trouver la différence entre deux ensembles.
Un exemple
Nous allons examiner un exemple de la différence entre les deux ensembles. Pour voir comment la différence de deux ensembles forme un nouvel ensemble, considérons les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}. Pour trouver la différence A – B de ces deux ensembles, nous commençons par écrire tous les éléments de A, puis nous enlevons tout élément de A qui est également un élément de B. Puisque A partage les éléments 3, 4 et 5 avec B, cela nous donne la différence d’ensemble A – B = {1, 2}.
L’ordre est important
Tout comme les différences 4 – 7 et 7 – 4 nous donnent des réponses différentes, nous devons faire attention à l’ordre dans lequel nous calculons la différence fixée. Pour utiliser un terme technique issu des mathématiques, nous dirions que l’opération de la différence fixée n’est pas commutative. Cela signifie qu’en général, nous ne pouvons pas changer l’ordre de la différence de deux ensembles et nous attendre au même résultat. Nous pouvons dire plus précisément que pour tous les ensembles A et B, A – B n’est pas égal à B – A.
Pour le constater, reportez-vous à l’exemple ci-dessus. Nous avons calculé que pour les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}, la différence A – B = {1, 2 }. Pour comparer cela à B – A, nous commençons par les éléments de B, qui sont 3, 4, 5, 6, 7, 8, puis nous enlevons les 3, 4 et 5 parce qu’ils sont en commun avec A. Le résultat est B – A = {6, 7, 8 }. Cet exemple nous montre clairement que A – B n’est pas égal à B – A.
Le complément
Une sorte de différence est suffisamment importante pour justifier son propre nom et symbole spécial. C’est ce qu’on appelle le complément, et il est utilisé pour la différence d’ensemble lorsque le premier ensemble est l’ensemble universel. Le complément de A est donné par l’expression U – A. Cela fait référence à l’ensemble de tous les éléments de l’ensemble universel qui ne sont pas des éléments de A. Comme il est entendu que l’ensemble des éléments parmi lesquels nous pouvons choisir est tiré de l’ensemble universel, nous pouvons simplement dire que le complément de A est l’ensemble composé d’éléments qui ne sont pas des éléments de A.
Le complément d’un ensemble est relatif à l’ensemble universel avec lequel nous travaillons. Avec A = {1, 2, 3} et U = {1, 2 ,3, 4, 5}, le complément de A est {4, 5}. Si notre ensemble universel est différent, disons U = {-3, -2, 0, 1, 2, 3 }, alors le complément de A {-3, -2, -1, 0}. Veillez toujours à faire attention à l’ensemble universel utilisé.
Notation pour le complément
Le mot « complément » commence par la lettre C et est donc utilisé dans la notation. Le complément de l’ensemble A s’écrit AC. Nous pouvons donc exprimer la définition du complément en symboles comme : AC = U – A.
Une autre façon couramment utilisée pour désigner le complément d’un ensemble est l’apostrophe, qui s’écrit « A ».
Autres identités impliquant la différence et les compléments
Il existe de nombreuses identités fixes qui impliquent l’utilisation des opérations de différence et de complément. Certaines identités combinent d’autres opérations d’ensemble telles que l’intersection et l’union. Quelques-unes des plus importantes sont mentionnées ci-dessous. Pour tous les ensembles A, et B et D, nous avons :
- A – A =∅
- A – ∅ = A
- ∅ – A = ∅
- A – U = ∅
- (AC)C = A
- Loi DeMorgan I : (A ∩ B)C = AC ∪ BC
- Loi DeMorgan II : (A ∪ B)C = AC ∩ BC