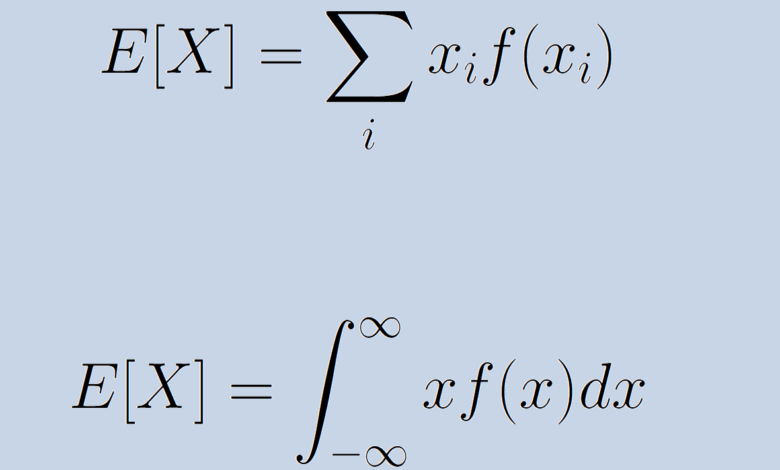
Contents
Vous êtes à un carnaval et vous voyez un jeu. Pour 2 $, vous lancez un dé à six faces standard. Si le chiffre affiché est un six, vous gagnez 10 $, sinon, vous ne gagnez rien. Si vous essayez de gagner de l’argent, avez-vous intérêt à jouer le jeu ? Pour répondre à une telle question, nous avons besoin du concept de valeur attendue.
La valeur attendue peut vraiment être considérée comme la moyenne d’une variable aléatoire. Cela signifie que si vous avez effectué une expérience de probabilité à plusieurs reprises, en gardant une trace des résultats, la valeur attendue est la moyenne de toutes les valeurs obtenues. La valeur escomptée est ce que vous devez prévoir à long terme dans de nombreux essais d’un jeu de hasard.
Comment calculer la valeur escomptée
Le jeu de carnaval mentionné ci-dessus est un exemple de variable aléatoire discrète. La variable n’est pas continue et chaque résultat nous parvient sous la forme d’un nombre qui peut être séparé des autres. Pour trouver la valeur attendue d’un jeu dont les résultats sont x1, x2, …, xn avec des probabilités p1, p2, … pn, calculer :
x1p1 + x2p2 + … + xnpn.
Pour le jeu ci-dessus, vous avez une probabilité de 5/6 de ne rien gagner. La valeur de ce résultat est de -2 puisque vous avez dépensé 2 $ pour jouer au jeu. Un six a une probabilité de 1/6 de se présenter, et cette valeur a un résultat de 8. Pourquoi 8 et non 10 ? Là encore, nous devons tenir compte des 2 dollars que nous avons payés pour jouer, et 10 – 2 = 8.
Maintenant, il suffit d’intégrer ces valeurs et ces probabilités dans la formule de la valeur attendue et on obtient le résultat : -2 (5/6) + 8 (1/6) = -1/3. Cela signifie qu’à long terme, vous devriez vous attendre à perdre en moyenne environ 33 cents chaque fois que vous jouez à ce jeu. Oui, vous gagnerez parfois. Mais vous perdrez plus souvent.
Supposons maintenant que le jeu du carnaval ait été légèrement modifié. Pour le même prix d’entrée de 2 $, si le numéro affiché est un six, vous gagnez 12 $, sinon, vous ne gagnez rien. La valeur attendue de ce jeu est de -2 (5/6) + 10 (1/6) = 0. À long terme, vous ne perdrez pas d’argent, mais vous n’en gagnerez pas. Ne vous attendez pas à voir un jeu avec ces chiffres à votre fête foraine locale. Si, à long terme, vous ne perdez pas d’argent, alors la fête foraine n’en gagnera pas.
Valeur escomptée au casino
Maintenant, tournez-vous vers le casino. De la même manière qu’auparavant, nous pouvons calculer la valeur attendue des jeux de hasard tels que la roulette. Aux États-Unis, une roulette comporte 38 cases numérotées de 1 à 36, 0 et 00. La moitié des 1-36 sont rouges, l’autre moitié sont noires. Le 0 et le 00 sont tous deux verts. Une bille atterrit au hasard dans l’une des fentes, et les paris sont placés sur l’endroit où la bille atterrira.
L’un des paris les plus simples est de parier sur le rouge. Ici, si vous pariez 1 $ et que la bille atterrit sur un numéro rouge dans la roue, vous gagnez 2 $. Si la bille atterrit sur un espace noir ou vert dans la roue, vous ne gagnez rien. Quelle est la valeur attendue d’un tel pari ? Comme il y a 18 cases rouges, il y a une probabilité de 18/38 de gagner, avec un gain net de 1 $. Il y a une probabilité de 20/38 de perdre votre mise initiale de 1 $. La valeur attendue de cette mise à la roulette est de 1 (18/38) + (-1) (20/38) = -2/38, soit environ 5,3 cents. Ici, la maison a un léger avantage (comme pour tous les jeux de casino).
La valeur escomptée et la loterie
Autre exemple : la loterie. Bien que des millions puissent être gagnés pour le prix d’un billet d’un dollar, la valeur attendue d’un jeu de loterie montre à quel point il est construit de manière injuste. Supposons que pour 1 $, vous choisissiez six numéros de 1 à 48. La probabilité de choisir correctement les six numéros est de 1/12 271 512. Si vous gagnez un million de dollars pour avoir choisi les six bons numéros, quelle est la valeur escomptée de cette loterie ? Les valeurs possibles sont de -1$ pour perdre et de 999 999$ pour gagner (là encore, il faut tenir compte du coût du jeu et le soustraire des gains). Cela nous donne une valeur escomptée de :
(-1)(12,271,511/12,271,512) + (999,999)(1/12,271,512) = -.918
Ainsi, si vous jouez à la loterie encore et encore, à long terme, vous perdez environ 92 cents – soit la quasi-totalité du prix de votre billet – à chaque fois que vous jouez.
Variables aléatoires continues
Tous les exemples ci-dessus portent sur une variable aléatoire discrète. Cependant, il est également possible de définir la valeur attendue pour une variable aléatoire continue. Tout ce que nous devons faire dans ce cas est de remplacer la somme dans notre formule par une intégrale.
Sur le long terme
Il est important de se rappeler que la valeur attendue est la moyenne après de nombreux essais d’un processus aléatoire. À court terme, la moyenne d’une variable aléatoire peut varier de manière significative par rapport à la valeur attendue.