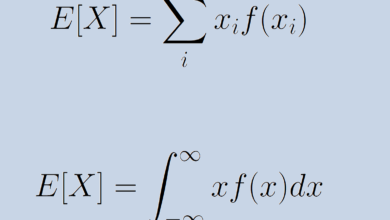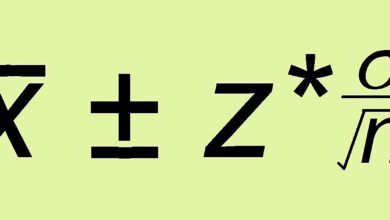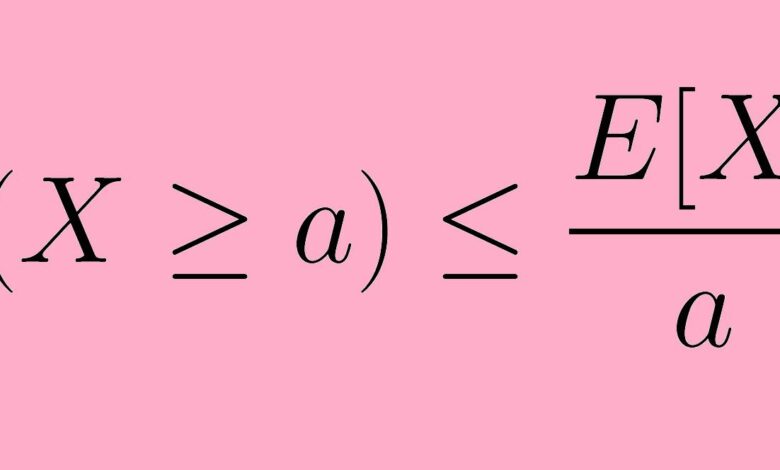
Contents
L’inégalité de Markov est un résultat utile dans la probabilité qui donne des informations sur une distribution de probabilité. Ce qui est remarquable, c’est que l’inégalité est valable pour toute distribution ayant des valeurs positives, quelles que soient ses autres caractéristiques. L’inégalité de Markov donne une limite supérieure pour le pourcentage de la distribution qui se situe au-dessus d’une valeur particulière.
Déclaration de Markov sur l’inégalité
Selon l’inégalité de Markov, pour une variable aléatoire positive X et tout nombre réel positif a, la probabilité que X soit supérieur ou égal à a est inférieure ou égale à la valeur attendue de X divisée par a.
La description ci-dessus peut être énoncée de manière plus succincte en utilisant la notation mathématique. En symboles, nous écrivons l’inégalité de Markov comme :
P (X ≥ a) ≤ E( X) /a
Illustration de l’inégalité
Pour illustrer l’inégalité, supposons que nous ayons une distribution avec des valeurs non négatives (comme une distribution chi carré). Si cette variable aléatoire X a une valeur attendue de 3, nous examinerons les probabilités pour quelques valeurs de a.
- Pour a = 10, l’inégalité de Markov dit que P (X ≥ 10) ≤ 3/10 = 30%. Il y a donc une probabilité de 30% que X soit supérieur à 10.
- Pour a = 30, l’inégalité de Markov dit que P (X ≥ 30) ≤ 3/30 = 10%. Il y a donc une probabilité de 10 % que X soit supérieur à 30.
- Pour a = 3, l’inégalité de Markov dit que P (X ≥ 3) ≤ 3/3 = 1. Les événements ayant une probabilité de 1 = 100% sont certains. Cela signifie donc qu’une certaine valeur de la variable aléatoire est supérieure ou égale à 3, ce qui ne devrait pas être trop surprenant. Si toutes les valeurs de X étaient inférieures à 3, alors la valeur attendue serait également inférieure à 3.
- Plus la valeur de a augmente, plus le quotient E(X)/a diminue. Cela signifie que la probabilité est très faible que X soit très, très grande. Là encore, avec une valeur attendue de 3, on ne s’attendrait pas à ce qu’il y ait une grande partie de la distribution avec des valeurs très grandes.
Utilisation de l’inégalité
Si nous en savons plus sur la distribution avec laquelle nous travaillons, nous pouvons généralement améliorer l’inégalité de Markov. L’intérêt de l’utiliser est qu’il est valable pour toute distribution ayant des valeurs non négatives.
Par exemple, si nous connaissons la taille moyenne des élèves d’une école primaire. L’inégalité de Markov nous dit que pas plus d’un sixième des élèves ne peut avoir une taille supérieure à six fois la taille moyenne.
L’autre utilisation majeure de l’inégalité de Markov est de prouver l’inégalité de Tchebychev. C’est pourquoi l’appellation « inégalité de Tchebychev » est également appliquée à l’inégalité de Markov. La confusion de la dénomination des inégalités est également due à des circonstances historiques. Andrey Markov était l’élève de Pafnuty Chebyshev. Le travail de Tchebychev contient l’inégalité qui est attribuée à Markov.