Contents
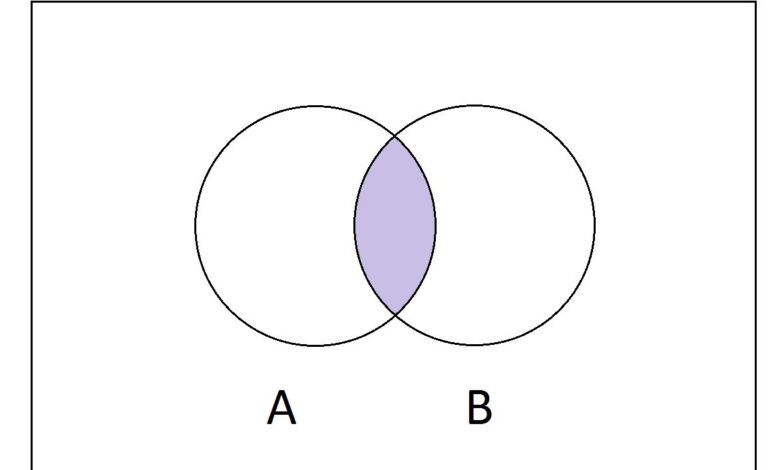
En matière de théorie des ensembles, il existe un certain nombre d’opérations permettant de créer de nouveaux ensembles à partir d’anciens. L’une des opérations les plus courantes est celle de l’intersection. En termes simples, l’intersection de deux ensembles A et B est l’ensemble de tous les éléments que A et B ont en commun.
Nous examinerons les détails concernant l’intersection dans la théorie des ensembles. Comme nous le verrons, le mot clé ici est le mot « et ».
Un exemple
Pour un exemple de la façon dont l’intersection de deux ensembles forme un nouvel ensemble, considérons les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}. Pour trouver l’intersection de ces deux ensembles, nous devons découvrir les éléments qu’ils ont en commun. Les nombres 3, 4, 5 sont des éléments des deux ensembles, donc l’intersection de A et B est {3. 4. 5].
Notation pour l’intersection
En plus de comprendre les concepts relatifs aux opérations de la théorie des ensembles, il est important de pouvoir lire les symboles utilisés pour désigner ces opérations. Le symbole d’intersection est parfois remplacé par le mot « et » entre deux ensembles. Ce mot suggère la notation plus compacte pour une intersection qui est généralement utilisée.
Le symbole utilisé pour l’intersection des deux ensembles A et B est donné par A ∩ B. Une façon de se rappeler que ce symbole ∩ fait référence à l’intersection est de remarquer sa ressemblance avec une majuscule A, qui est l’abréviation du mot « et ».
Pour voir cette notation en action, reportez-vous à l’exemple ci-dessus. Ici, nous avions les ensembles A = {1, 2, 3, 4, 5} et B = {3, 4, 5, 6, 7, 8}. Nous écririons donc l’équation de l’ensemble A ∩ B = {3, 4, 5}.
Intersection avec l’ensemble vide
Une identité de base qui implique l’intersection nous montre ce qui se passe lorsque nous prenons l’intersection d’un ensemble quelconque avec l’ensemble vide, désigné par le numéro 8709. L’ensemble vide est l’ensemble sans éléments. S’il n’y a pas d’éléments dans au moins un des ensembles dont nous essayons de trouver l’intersection, alors les deux ensembles n’ont pas d’éléments en commun. En d’autres termes, l’intersection de n’importe quel ensemble avec l’ensemble vide nous donnera l’ensemble vide.
Cette identité devient encore plus compacte avec l’utilisation de notre notation. Nous avons l’identité : A ∩ ∅ = ∅.
Intersection avec l’ensemble universel
Pour l’autre extrême, que se passe-t-il lorsque nous examinons l’intersection d’un ensemble avec l’ensemble universel ? Comme le mot « univers » est utilisé en astronomie pour tout signifier, l’ensemble universel contient tous les éléments. Il s’ensuit que chaque élément de notre ensemble est également un élément de l’ensemble universel. Ainsi, l’intersection d’un ensemble quelconque avec l’ensemble universel est l’ensemble avec lequel nous avons commencé.
Une fois de plus, notre notation vient à la rescousse pour exprimer plus succinctement cette identité. Pour tout ensemble A et l’ensemble universel U, A ∩ U = A.
Autres identités impliquant l’intersection
Il y a beaucoup d’autres équations qui impliquent l’utilisation de l’opération d’intersection. Bien sûr, il est toujours bon de s’entraîner à utiliser le langage de la théorie des ensembles. Pour tous les ensembles A, et B et D que nous avons :
- Propriété réflexe : A ∩ A =A
- Propriété commutative : A ∩ B = B ∩ A
- Propriété associative : (A ∩ B) ∩ D =A ∩ (B ∩ D)
- La propriété distributive : (A ∪ B) ∩ D = (A ∩ D)∪ (B ∩ D)
- Loi DeMorgan I : (A ∩ B)C = AC ∪ BC
- Loi DeMorgan II : (A ∪ B)C = AC ∩ BC