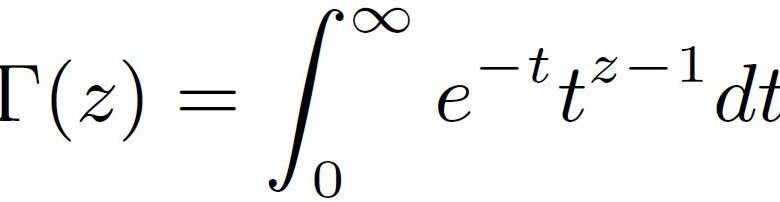
Contents
La fonction gamma est une fonction un peu compliquée. Cette fonction est utilisée en statistique mathématique. Elle peut être considérée comme un moyen de généraliser le factoriel.
La fonction factuelle
Nous apprenons assez tôt dans notre carrière mathématique que le factoriel, défini pour des entiers non négatifs n, est une façon de décrire les multiplications répétées. Elle est indiquée par l’utilisation d’un point d’exclamation. Par exemple.
3 ! = 3 x 2 x 1 = 6 et 5 ! = 5 x 4 x 3 x 2 x 1 = 120.
La seule exception à cette définition est la factorielle zéro, où 0 ! = 1. En examinant ces valeurs pour la factorielle, nous pourrions associer n avec n ! Cela nous donnerait les points (0, 1), (1, 1), (2, 2), (3, 6), (4, 24), (5, 120), (6, 720), et ainsi de suite.
Si nous traçons ces points, nous pouvons poser quelques questions :
- Y a-t-il un moyen de relier les points et de remplir le graphique pour plus de valeurs ?
- Existe-t-il une fonction qui correspond à la factorielle pour les nombres entiers non négatifs, mais qui est définie sur un sous-ensemble plus important des nombres réels.
La réponse à ces questions est « La fonction gamma ».
Définition de la fonction gamma
La définition de la fonction gamma est très complexe. Elle implique une formule d’apparence compliquée qui semble très étrange. La fonction gamma utilise un certain calcul dans sa définition, ainsi que le nombre e. Contrairement aux fonctions plus familières telles que les polynômes ou les fonctions trigonométriques, la fonction gamma est définie comme l’intégrale impropre d’une autre fonction.
La fonction gamma est désignée par une lettre majuscule gamma de l’alphabet grec. Cela ressemble à ce qui suit : Γ( z )
Caractéristiques de la fonction gamma
La définition de la fonction gamma peut être utilisée pour démontrer un certain nombre d’identités. L’une des plus importantes est la suivante : Γ( z + 1 ) = z Γ( z ). Nous pouvons utiliser cette définition et le fait que Γ( 1 ) = 1 du calcul direct :
Γ( n ) = (n – 1) Γ( n – 1 ) = (n – 1) (n – 2) Γ( n – 2 ) = (n – 1) !
La formule ci-dessus établit le lien entre la fonction factorielle et la fonction gamma. Elle nous donne également une autre raison pour laquelle il est logique de définir la valeur de zéro factoriel comme étant égale à 1.
Mais nous ne devons pas seulement entrer des nombres entiers dans la fonction gamma. Tout nombre complexe qui n’est pas un nombre entier négatif se trouve dans le domaine de la fonction gamma. Cela signifie que nous pouvons étendre la factorielle à des nombres autres que les entiers non négatifs. Parmi ces valeurs, l’un des résultats les plus connus (et les plus surprenants) est que Γ( 1/2 ) = √π.
Un autre résultat similaire au précédent est que Γ( 1/2 ) = -2π. En effet, la fonction gamma produit toujours une sortie d’un multiple de la racine carrée de pi lorsqu’un multiple impair de 1/2 est entré dans la fonction.
Utilisation de la fonction gamma
La fonction gamma apparaît dans de nombreux domaines des mathématiques, apparemment sans rapport entre eux. En particulier, la généralisation de la factorielle fournie par la fonction gamma est utile dans certains problèmes de combinatoire et de probabilité. Certaines distributions de probabilités sont définies directement en termes de fonction gamma. Par exemple, la distribution gamma est énoncée en termes de fonction gamma. Cette distribution peut être utilisée pour modéliser l’intervalle de temps entre les tremblements de terre. La distribution de Student, qui peut être utilisée pour les données pour lesquelles nous avons un écart type de population inconnu, et la distribution du khi-deux sont également définies en termes de fonction gamma.