Contents
Les distributions de données et les distributions de probabilités n’ont pas toutes la même forme. Certaines sont asymétriques et biaisées vers la gauche ou vers la droite. D’autres distributions sont bimodales et comportent deux pics. Une autre caractéristique à prendre en compte lorsque l’on parle de distribution est la forme des queues de la distribution à l’extrême gauche et à l’extrême droite. La kurtosis est la mesure de l’épaisseur ou de la lourdeur des queues d’une distribution. L’aplatissement d’une distribution fait partie de l’une des trois catégories de classification :
- Mesokurtic
- Leptokurtic
- Platykurtic
Nous examinerons chacune de ces classifications à tour de rôle. Notre examen de ces catégories ne sera pas aussi précis que nous pourrions l’être si nous utilisions la définition mathématique technique de l’aplatissement.
Mesokurtic
La kurtose est généralement mesurée par rapport à la distribution normale. Une distribution dont les queues ont à peu près la même forme que toute distribution normale, et pas seulement la distribution normale standard, est dite mésokurtique. L’aplatissement d’une distribution mésokurtique n’est ni élevé ni faible, mais il est plutôt considéré comme une référence pour les deux autres classifications.
Outre les distributions normales, les distributions binomiales pour lesquelles p est proche de 1/2 sont considérées comme mésokurtiques.
Leptokurtic
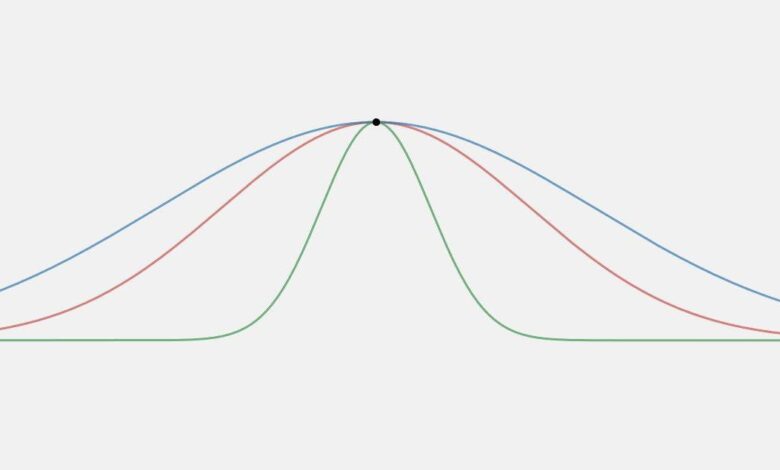
Une distribution leptokurtique est une distribution qui présente une kurtose plus importante qu’une distribution mésokurtique. Les distributions leptokurtiques sont parfois identifiées par des pics minces et hauts. Les queues de ces distributions, à droite et à gauche, sont épaisses et lourdes. Les distributions leptokurtiques sont nommées par le préfixe « lepto » qui signifie « maigre ».
Il existe de nombreux exemples de distributions leptokurtiques. L’une des distributions leptokurtiques les plus connues est la distribution t de Student.
Platykurtic
La troisième classification pour l’aplatissement est la platykurtique. Les distributions platykurtiques sont celles qui ont des queues fines. Elles possèdent souvent un pic inférieur à une distribution mésokurtique. Le nom de ces types de distributions vient de la signification du préfixe « platy » qui signifie « large ».
Toutes les distributions uniformes sont platykurtiques. En outre, la distribution discrète des probabilités d’un seul coup de pièce de monnaie est platykurtique.
Calcul de la kurtosis
Ces classifications de l’aplatissement sont encore quelque peu subjectives et qualitatives. Si nous pouvons constater qu’une distribution a des queues plus épaisses qu’une distribution normale, que se passe-t-il si nous n’avons pas le graphique d’une distribution normale pour la comparer ? Et si nous voulons dire qu’une distribution est plus leptokurtique qu’une autre ?
Pour répondre à ce genre de questions, nous avons besoin non seulement d’une description qualitative de l’aplatissement, mais aussi d’une mesure quantitative. La formule utilisée est σ4/σ4 où μ4 est le quatrième moment de Pearson sur la moyenne et sigma est l’écart-type.
Excès de kurtosis
Maintenant que nous disposons d’un moyen de calculer l’aplatissement, nous pouvons comparer les valeurs obtenues plutôt que les formes. On constate que la distribution normale présente une aplatissement de trois. Cela devient maintenant notre base pour les distributions mésokurtiques. Une distribution avec une kurtosis supérieure à trois est leptokurtique et une distribution avec une kurtosis inférieure à trois est platykurtique.
Comme nous traitons une distribution mésokurtique comme base de référence pour nos autres distributions, nous pouvons en soustraire trois de notre calcul standard de l’aplatissement. La formule μ4/σ4 – 3 est la formule pour l’excès de kurtosis. Nous pourrions alors classer une distribution à partir de son excès de kurtosis :
- Les distributions mésokurtiques ont une kurtose excessive de zéro.
- Les distributions platykurtiques présentent un excès de kurtosis négatif.
- Les distributions leptokurtiques présentent un excès de kurtosis positif.
Une note sur le nom
Le mot « kurtosis » semble étrange en première ou deuxième lecture. Il a en fait un sens, mais il faut connaître le grec pour le reconnaître. Kurtosis est dérivé d’une translittération du mot grec kurtos. Ce mot grec a le sens d' »arqué » ou de « bombé », ce qui en fait une description appropriée du concept connu sous le nom de kurtosis.