Contents
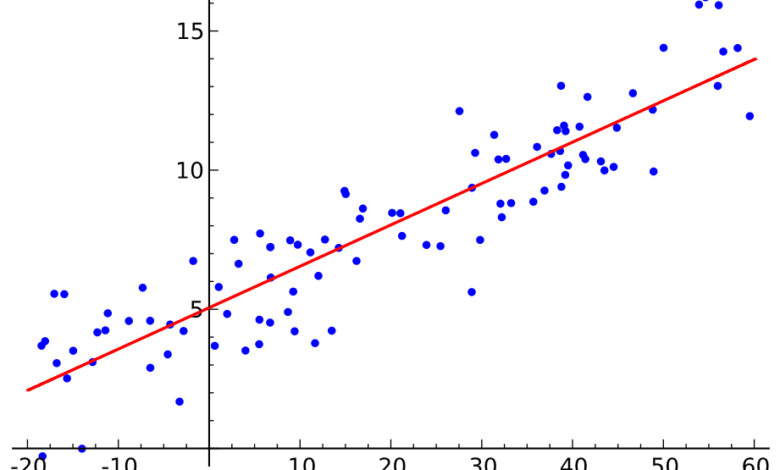
Un nuage de points est un type de graphique qui est utilisé pour représenter des données appariées. La variable explicative est tracée le long de l’axe horizontal et la variable réponse est tracée le long de l’axe vertical. L’une des raisons d’utiliser ce type de graphique est de rechercher des relations entre les variables.
Le schéma le plus élémentaire à rechercher dans un ensemble de données appariées est celui d’une ligne droite. En passant par deux points quelconques, on peut tracer une ligne droite. S’il y a plus de deux points dans notre nuage de points, la plupart du temps, nous ne pourrons plus tracer une ligne passant par chaque point. À la place, nous traçons une ligne qui passe par le milieu des points et affiche la tendance linéaire globale des données.
Lorsque nous examinons les points de notre graphique et que nous souhaitons tracer une ligne à travers ces points, une question se pose. Quelle ligne devrions-nous tracer ? Il existe un nombre infini de lignes qui pourraient être tracées. En utilisant nos seuls yeux, il est clair que chaque personne regardant le nuage de points pourrait produire une ligne légèrement différente. Cette ambiguïté pose un problème. Nous voulons disposer d’un moyen bien défini pour que chacun obtienne la même ligne. L’objectif est d’avoir une description mathématiquement précise de la ligne à tracer. La ligne de régression des moindres carrés est une telle ligne passant par nos points de données.
Les moindres carrés
Le nom de la ligne des moindres carrés explique ce qu’elle fait. On commence par un ensemble de points dont les coordonnées sont données par (xi, yi). Toute ligne droite passera entre ces points et ira soit au-dessus soit en dessous de chacun d’entre eux. Nous pouvons calculer les distances entre ces points et la ligne en choisissant une valeur de x et en soustrayant ensuite la coordonnée y observée qui correspond à ce x de la coordonnée y de notre ligne.
Des lignes différentes passant par le même ensemble de points donneraient un ensemble différent de distances. Nous voulons que ces distances soient aussi faibles que possible. Mais il y a un problème. Comme nos distances peuvent être positives ou négatives, la somme totale de toutes ces distances s’annulera. La somme des distances sera toujours égale à zéro.
La solution à ce problème est d’éliminer tous les nombres négatifs en quadrillant les distances entre les points et la ligne. On obtient ainsi une collection de nombres non négatifs. L’objectif que nous avions de trouver une ligne qui corresponde le mieux à la réalité est le même que de rendre la somme de ces carrés aussi petite que possible. Le calcul vient à la rescousse ici. Le processus de différenciation dans le calcul permet de minimiser la somme des carrés des distances d’une ligne donnée. C’est ce qui explique l’expression « moindres carrés » dans notre nom pour cette ligne.
Ligne de Best Fit
Puisque la ligne des moindres carrés minimise les distances au carré entre la ligne et nos points, nous pouvons considérer cette ligne comme celle qui correspond le mieux à nos données. C’est pourquoi la ligne des moindres carrés est également connue comme la ligne du meilleur ajustement. Parmi toutes les lignes possibles qui pourraient être tracées, la ligne des moindres carrés est la plus proche de l’ensemble des données. Cela peut signifier que notre ligne n’atteindra aucun des points de notre ensemble de données.
Caractéristiques de la ligne des moindres carrés
Il y a quelques caractéristiques que la moindre ligne carrée possède. Le premier élément d’intérêt concerne la pente de notre ligne. La pente a un lien avec le coefficient de corrélation de nos données. En fait, la pente de la droite est égale à r(sy/sx). Ici, s x indique l’écart type des coordonnées x et s y l’écart type des coordonnées y de nos données. Le signe du coefficient de corrélation est directement lié au signe de la pente de notre ligne des moindres carrés.
Une autre caractéristique de la ligne des moindres carrés concerne un point qu’elle traverse. Bien que l’interception y d’une ligne des moindres carrés ne soit pas intéressante d’un point de vue statistique, il y a un point qui l’est. Chaque ligne des moindres carrés passe par le point central des données. Ce point central a une coordonnée x qui est la moyenne des valeurs x et une coordonnée y qui est la moyenne des valeurs y.