Contents
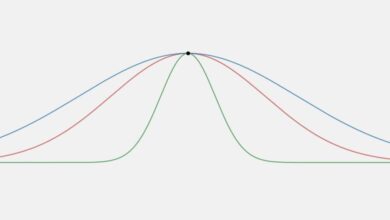
Certaines distributions de données, telles que la courbe en cloche ou la distribution normale, sont symétriques. Cela signifie que la droite et la gauche de la distribution sont des images parfaitement symétriques l’une de l’autre. Toutes les distributions de données ne sont pas symétriques. Les ensembles de données qui ne sont pas symétriques sont dits asymétriques. La mesure de l’asymétrie d’une distribution est appelée asymétrie.
La moyenne, la médiane et le mode sont tous des mesures du centre d’un ensemble de données. L’asymétrie des données peut être déterminée par la façon dont ces quantités sont liées les unes aux autres.
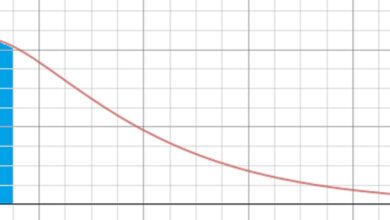
Déformé à droite
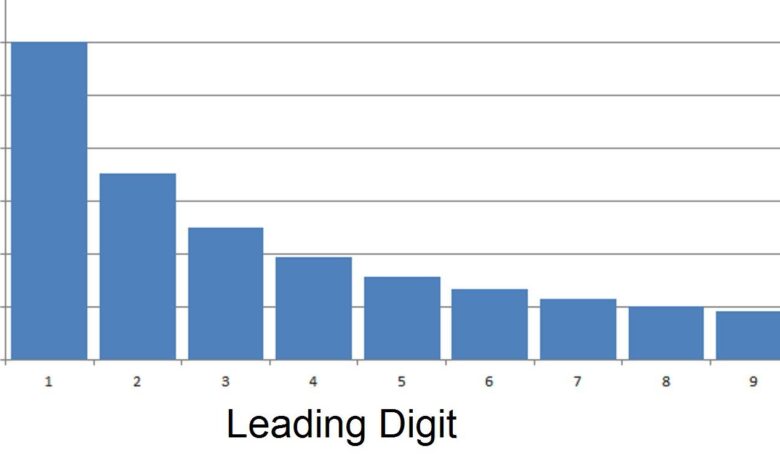
Les données qui sont biaisées vers la droite ont une longue queue qui s’étend vers la droite. Une autre façon de parler d’un ensemble de données biaisées vers la droite est de dire qu’il est positivement biaisé. Dans cette situation, la moyenne et la médiane sont toutes deux supérieures au mode. En règle générale, la plupart du temps, pour des données biaisées vers la droite, la moyenne sera supérieure à la médiane. En résumé, pour un ensemble de données biaisées vers la droite :
- Toujours : signifie plus grand que le mode
- Toujours : la médiane est supérieure au mode
- La plupart du temps : moyenne supérieure à la médiane
A gauche
La situation s’inverse lorsque nous traitons des données biaisées vers la gauche. Les données qui sont biaisées vers la gauche ont une longue queue qui s’étend vers la gauche. Une autre façon de parler d’un ensemble de données biaisées vers la gauche est de dire qu’il est biaisé négativement. Dans cette situation, la moyenne et la médiane sont toutes deux inférieures au mode. En règle générale, la plupart du temps, pour des données biaisées vers la gauche, la moyenne sera inférieure à la médiane. En résumé, pour un ensemble de données biaisées vers la gauche :
- Toujours : signifie moins que le mode
- Toujours : la médiane est inférieure au mode
- La plupart du temps : moyenne inférieure à la médiane
Mesures de l’asymétrie
C’est une chose d’examiner deux ensembles de données et de déterminer que l’un est symétrique et l’autre asymétrique. C’est une autre chose de regarder deux ensembles de données asymétriques et de dire que l’un est plus asymétrique que l’autre. Il peut être très subjectif de déterminer lequel est le plus asymétrique en regardant simplement le graphique de la distribution. C’est pourquoi il existe des moyens de calculer numériquement la mesure de l’asymétrie.
Une mesure de l’asymétrie, appelée premier coefficient d’asymétrie de Pearson, consiste à soustraire la moyenne du mode, puis à diviser cette différence par l’écart-type des données. La raison pour laquelle on divise la différence est que l’on a une quantité sans dimension. Cela explique pourquoi les données biaisées vers la droite ont une asymétrie positive. Si l’ensemble de données est biaisé vers la droite, la moyenne est supérieure au mode, et donc la soustraction du mode de la moyenne donne un nombre positif. Un argument similaire explique pourquoi les données biaisées vers la gauche ont une asymétrie négative.
Le deuxième coefficient d’asymétrie de Pearson est également utilisé pour mesurer l’asymétrie d’un ensemble de données. Pour cette quantité, nous soustrayons le mode de la médiane, multiplions ce nombre par trois et divisons ensuite par l’écart-type.
Applications des données biaisées
Les données faussées se produisent tout naturellement dans diverses situations. Les revenus sont biaisés vers la droite parce que même quelques individus qui gagnent des millions de dollars peuvent grandement affecter la moyenne, et il n’y a pas de revenus négatifs. De même, les données concernant la durée de vie d’un produit, comme une marque d’ampoule, sont biaisées vers la droite. Dans ce cas, la plus petite durée de vie possible est de zéro, et les ampoules longue durée confèrent une asymétrie positive aux données.