Contents
Quand rien ne peut être quelque chose ? C’est une question stupide et assez paradoxale. Dans le domaine mathématique de la théorie des ensembles, il est courant que rien ne soit autre chose que rien. Comment cela peut-il être ?
Lorsque nous formons un ensemble sans éléments, nous n’avons plus rien. Nous avons un ensemble qui ne contient rien. Il existe un nom spécial pour l’ensemble qui ne contient pas d’éléments. C’est ce qu’on appelle l’ensemble vide ou nul.
Une différence subtile
La définition de l’ensemble vide est assez subtile et demande un peu de réflexion. Il est important de se rappeler que nous considérons un ensemble comme une collection d’éléments. L’ensemble lui-même est différent des éléments qu’il contient.
Par exemple, nous allons examiner {5}, qui est un ensemble contenant l’élément 5. L’ensemble {5} n’est pas un nombre. Il s’agit d’un ensemble contenant le chiffre 5 comme élément, alors que 5 est un chiffre.
De la même manière, l’ensemble vide n’est pas rien. C’est plutôt l’ensemble sans éléments. Il est utile de considérer les ensembles comme des conteneurs, et les éléments sont les choses que nous y mettons. Un conteneur vide est toujours un conteneur et est analogue à l’ensemble vide.
L’unicité de l’ensemble vide
L’ensemble vide est unique, c’est pourquoi il est tout à fait approprié de parler de l’ensemble vide, plutôt que d’un ensemble vide. C’est ce qui distingue l’ensemble vide des autres ensembles. Il existe une infinité d’ensembles contenant un seul élément. Les ensembles {a}, {1}, {b} et {123} ont chacun un élément, et sont donc équivalents les uns aux autres. Comme les éléments eux-mêmes sont différents les uns des autres, les ensembles ne sont pas égaux.
Les exemples ci-dessus n’ont rien de particulier, chacun ayant un élément. À une exception près, pour tout nombre de comptage ou à l’infini, il existe une infinité d’ensembles de cette taille. L’exception concerne le nombre zéro. Il n’y a qu’un seul ensemble, l’ensemble vide, qui ne contient aucun élément.
La preuve mathématique de ce fait n’est pas difficile à apporter. Nous supposons d’abord que l’ensemble vide n’est pas unique, qu’il existe deux ensembles sans éléments, puis nous utilisons quelques propriétés de la théorie des ensembles pour montrer que cette hypothèse implique une contradiction.
Notation et terminologie pour l’ensemble vide
L’ensemble vide est indiqué par le symbole ∅, qui provient d’un symbole similaire de l’alphabet danois. Certains livres font référence à l’ensemble vide par son autre nom d’ensemble nul.
Propriétés de l’ensemble vide
Comme il n’y a qu’un seul ensemble vide, il est intéressant de voir ce qui se passe lorsque les opérations d’intersection, d’union et de complément sont utilisées avec l’ensemble vide et un ensemble général que nous désignerons par X. Il est également intéressant de considérer un sous-ensemble de l’ensemble vide et de se demander quand l’ensemble vide est un sous-ensemble. Ces faits sont rassemblés ci-dessous :
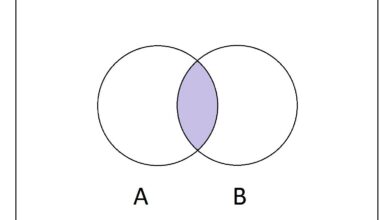
- L’intersection de tout ensemble avec l’ensemble vide est l’ensemble vide. En effet, l’ensemble vide ne contient aucun élément, et les deux ensembles n’ont donc aucun élément en commun. En symboles, on écrit X ∩ ∅ = ∅.
- L’union de tout ensemble avec l’ensemble vide est l’ensemble avec lequel nous avons commencé. C’est parce qu’il n’y a aucun élément dans l’ensemble vide, et donc nous n’ajoutons aucun élément à l’autre ensemble lorsque nous formons l’union. En symboles, nous écrivons X U ∅ = X.
- Le complément de l’ensemble vide est l’ensemble universel pour le cadre dans lequel nous travaillons. En effet, l’ensemble de tous les éléments qui ne font pas partie de l’ensemble vide n’est que l’ensemble de tous les éléments.
- L’ensemble vide est un sous-ensemble de n’importe quel ensemble. En effet, nous formons des sous-ensembles d’un ensemble X en sélectionnant (ou en ne sélectionnant pas) des éléments de X. Une option pour un sous-ensemble consiste à n’utiliser aucun élément de X. Cela nous donne l’ensemble vide.