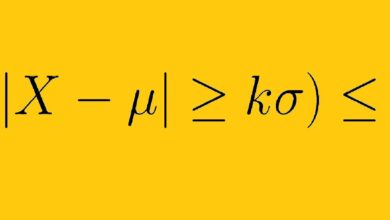Contents
Dans les statistiques inférentielles, les intervalles de confiance pour les proportions de la population reposent sur la distribution normale standard pour déterminer les paramètres inconnus d’une population donnée à partir d’un échantillon statistique de la population. L’une des raisons en est que pour des tailles d’échantillon appropriées, la distribution normale standard fait un excellent travail d’estimation d’une distribution binomiale. Ceci est remarquable car bien que la première distribution soit continue, la seconde est discrète.
Un certain nombre de questions doivent être abordées lors de la construction des intervalles de confiance pour les proportions. L’une d’entre elles concerne ce que l’on appelle un intervalle de confiance « plus quatre », qui donne un estimateur biaisé. Toutefois, cet estimateur d’une proportion de population inconnue donne de meilleurs résultats dans certaines situations que les estimateurs non biaisés, en particulier dans les situations où les données ne sont ni positives ni négatives.
Dans la plupart des cas, la meilleure tentative pour estimer une proportion de la population consiste à utiliser une proportion d’échantillon correspondante. Nous supposons qu’il existe une population dont la proportion p d’individus contenant un certain trait est inconnue, puis nous formons un échantillon aléatoire simple de taille n à partir de cette population. Parmi ces n individus, nous comptons le nombre Y qui possèdent le trait qui nous intéresse. Nous estimons maintenant p en utilisant notre échantillon. La proportion d’échantillon Y/n est un estimateur non biaisé de p.
Quand utiliser l’intervalle de confiance « plus quatre
Lorsque nous utilisons un intervalle de plus quatre, nous modifions l’estimateur de p. Nous le faisons en ajoutant quatre au nombre total d’observations, ce qui explique l’expression « plus quatre ». Nous répartissons ensuite ces quatre observations entre deux succès hypothétiques et deux échecs, ce qui signifie que nous ajoutons deux au nombre total de succès. Le résultat final est que nous remplaçons chaque instance de Y/n par (Y + 2)/(n + 4), et parfois cette fraction est dénotée par p avec un tilde au-dessus.
La proportion de l’échantillon fonctionne généralement très bien pour estimer une proportion de la population. Toutefois, dans certaines situations, nous devons modifier légèrement notre estimateur. La pratique statistique et la théorie mathématique montrent que la modification de l’intervalle plus quatre est appropriée pour atteindre cet objectif.
Une situation qui devrait nous amener à considérer un intervalle de plus quatre est un échantillon asymétrique. Souvent, la proportion de la population étant si petite ou si grande, la proportion de l’échantillon est également très proche de 0 ou très proche de 1. Dans ce type de situation, nous devrions envisager un intervalle de plus quatre.
Une autre raison d’utiliser un intervalle de plus quatre est que nous avons un échantillon de petite taille. Dans ce cas, l’intervalle plus quatre donne une meilleure estimation d’une proportion de la population que l’intervalle de confiance habituel pour une proportion.
Règles d’utilisation de l’intervalle de confiance « plus quatre
L’intervalle de confiance plus quatre est un moyen presque magique de calculer les statistiques inférentielles avec plus de précision, car en ajoutant simplement quatre observations imaginaires à un ensemble de données donné, deux réussites et deux échecs, il est possible de prédire avec plus de précision la proportion d’un ensemble de données qui correspond aux paramètres.
Cependant, l’intervalle de confiance plus quatre n’est pas toujours applicable à tous les problèmes. Il ne peut être utilisé que lorsque l’intervalle de confiance d’un ensemble de données est supérieur à 90 % et que la taille de l’échantillon de la population est d’au moins 10. Cependant, l’ensemble de données peut contenir un nombre quelconque de succès et d’échecs, bien qu’il fonctionne mieux lorsqu’il n’y a pas de succès ou d’échecs dans les données d’une population donnée.
Gardez à l’esprit que, contrairement aux calculs des statistiques régulières, les calculs des « statistiques inférentielles » reposent sur un échantillonnage de données pour déterminer les résultats les plus probables au sein d’une population. Bien que l’intervalle de confiance plus quatre corrige une marge d’erreur plus importante, cette marge doit tout de même être prise en compte pour fournir l’observation statistique la plus précise.