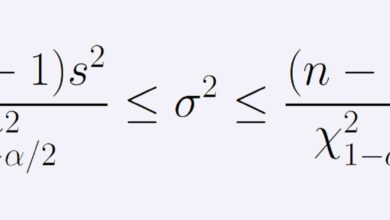
Contents
Si vous passez beaucoup de temps à vous occuper de statistiques, vous tombez rapidement sur l’expression « distribution de probabilité ». C’est là que l’on voit vraiment à quel point les domaines de la probabilité et des statistiques se chevauchent. Bien que cela puisse sembler technique, l’expression « distribution des probabilités » n’est en fait qu’une façon de parler de l’organisation d’une liste de probabilités. Une distribution de probabilités est une fonction ou une règle qui attribue des probabilités à chaque valeur d’une variable aléatoire. Dans certains cas, la distribution peut être énumérée. Dans d’autres cas, elle est présentée sous la forme d’un graphique.
Exemple
Supposons que nous lancions deux dés et que nous enregistrions ensuite la somme des dés. Des sommes allant de deux à 12 sont possibles. Chaque somme a une probabilité particulière de se produire. Nous pouvons simplement les énumérer comme suit :
- La somme de 2 a une probabilité de 1/36
- La somme de 3 a une probabilité de 2/36
- La somme de 4 a une probabilité de 3/36
- La somme de 5 a une probabilité de 4/36
- La somme de 6 a une probabilité de 5/36
- La somme de 7 a une probabilité de 6/36
- La somme de 8 a une probabilité de 5/36
- La somme de 9 a une probabilité de 4/36
- La somme de 10 a une probabilité de 3/36
- La somme de 11 a une probabilité de 2/36
- La somme de 12 a une probabilité de 1/36
Cette liste est une distribution de probabilité pour l’expérience de probabilité de lancer deux dés. Nous pouvons également considérer ce qui précède comme une distribution de probabilité de la variable aléatoire définie en examinant la somme des deux dés.
Graphique
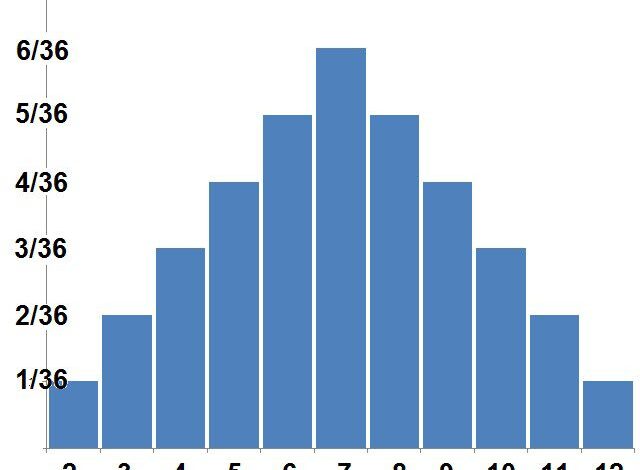
Une distribution de probabilités peut être représentée graphiquement, ce qui permet parfois de nous montrer des caractéristiques de la distribution qui n’étaient pas évidentes à la simple lecture de la liste des probabilités. La variable aléatoire est tracée sur l’axe des x et la probabilité correspondante sur l’axe des y. Pour une variable aléatoire discrète, nous aurons un histogramme. Pour une variable aléatoire continue, nous aurons l’intérieur d’une courbe lisse.
Les règles de probabilité sont toujours en vigueur, et elles se manifestent de quelques manières. Comme les probabilités sont supérieures ou égales à zéro, le graphique d’une distribution de probabilités doit avoir des coordonnées y non négatives. Une autre caractéristique des probabilités, à savoir que l’on est le maximum que la probabilité d’un événement peut être, se manifeste d’une autre manière.
Zone = Probabilité
Le graphique d’une distribution de probabilités est construit de telle manière que les zones représentent des probabilités. Pour une distribution de probabilités discrète, nous ne faisons en réalité que calculer les aires des rectangles. Dans le graphique ci-dessus, les aires des trois barres correspondant à quatre, cinq et six correspondent à la probabilité que la somme de nos dés soit de quatre, cinq ou six. Les aires de toutes les barres s’additionnent pour donner un total de un.
Dans la distribution normale standard ou courbe en cloche, nous avons une situation similaire. L’aire sous la courbe entre deux valeurs z correspond à la probabilité que notre variable se situe entre ces deux valeurs. Par exemple, l’aire sous la courbe en cloche pour -1 z.
Distributions importantes
Il existe littéralement une infinité de distributions de probabilités. Voici une liste de certaines des distributions les plus importantes :