Contents
Un cube est un type spécial de prisme rectangulaire dont la longueur, la largeur et la hauteur sont identiques. On peut aussi considérer un cube comme une boîte en carton composée de six carrés de même taille. Trouver la surface d’un cube est donc assez simple si vous connaissez les bonnes formules.
Normalement, pour trouver la surface ou le volume d’un prisme rectangulaire, il faut travailler avec une longueur, une largeur et une hauteur qui sont toutes différentes. Mais avec un cube, vous pouvez profiter du fait que tous les côtés sont égaux pour calculer facilement sa géométrie et trouver la surface.
Key Takeaways : Termes clés
- Cube: Un solide rectangulaire sur lequel la longueur, la largeur et la hauteur sont égales. Vous devez connaître la longueur, la hauteur et la largeur pour trouver la surface d’un cube.
- Superficie : La surface totale de la surface d’un objet tridimensionnel
- Volume : La quantité d’espace occupée par un objet tridimensionnel. Elle est mesurée en unités cubiques.
Trouver la surface d’un prisme rectangulaire
Avant de travailler à la recherche de la surface d’un cube, il est utile de revoir comment trouver la surface d’un prisme rectangulaire, car un cube est un type spécial de prisme rectangulaire.
Un rectangle en trois dimensions devient un prisme rectangulaire. Lorsque tous les côtés sont de dimensions égales, il devient un cube. Dans les deux cas, la détermination de la surface et du volume nécessite les mêmes formules.
Surface = 2(lh) + 2(lw) + 2(wh)
Volume = lhw
Ces formules vous permettront de trouver la surface d’un cube, ainsi que son volume et les relations géométriques au sein de la forme.
Surface d’un cube
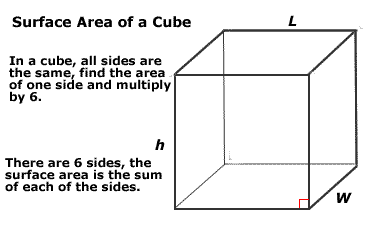
Dans l’exemple illustré, les côtés du cube sont représentés par L et h. Un cube a six côtés et la surface est la somme de la surface de tous les côtés. Vous savez également que, comme la figure est un cube, l’aire de chacun des six côtés sera la même.
Si vous utilisez l’équation traditionnelle d’un prisme rectangulaire, où SA signifie surface, vous l’auriez fait :
SA = 6(lw)
Cela signifie que la surface est égale à six (le nombre de côtés du cube) fois le produit de l (longueur) et de w (largeur). Puisque l et w sont représentés par L et h, vous l’auriez :
SA = 6(Lh)
Pour voir comment cela fonctionnerait avec un nombre, supposons que L est de 3 pouces et que h est de 3 pouces. Vous savez que L et h doivent être identiques car, par définition, dans un cube, toutes les faces sont identiques. La formule serait la suivante :
- SA = 6(Lh)
- SA = 6(3 x 3)
- SA = 6(9)
- SA = 54
La surface serait donc de 54 pouces carrés.
Volume d’un cube
Ce chiffre vous donne en fait la formule du volume d’un prisme rectangulaire :
V = L x l x h
Si vous deviez attribuer un numéro à chacune des variables, vous l’auriez peut-être fait :
L = 3 pouces
W = 3 pouces
h = 3 pouces
Rappelons que cela est dû au fait que toutes les faces d’un cube ont la même mesure. En utilisant la formule pour déterminer le volume, vous l’auriez fait :
- V = L x l x h
- V = 3 x 3 x 3
- V = 27
Le volume du cube serait donc de 27 pouces cubes. Notez également que puisque les côtés du cube sont tous de 3 pouces, vous pourriez également utiliser la formule plus traditionnelle pour trouver le volume d’un cube, où le symbole « ^ » signifie que vous élevez le nombre en exposant, dans ce cas, le nombre 3.
- V = s ^ 3
- V = 3 ^ 3 (ce qui signifie V = 3 x 3 x 3)
- V = 27
Relations en cube
Comme vous travaillez avec un cube, il existe certaines relations géométriques spécifiques. Par exemple, le segment de droite AB est perpendiculaire au segment BF. (Un segment de droite est la distance entre deux points sur une ligne.) Vous savez également que le segment de droite AB est parallèle au segment EF, ce que vous pouvez voir clairement en examinant la figure.
De plus, les segments AE et BC sont faussés. Les lignes obliques sont des lignes qui se trouvent dans des plans différents, ne sont pas parallèles et ne se croisent pas. Comme un cube est une forme tridimensionnelle, les segments de lignes AE et BC ne sont en effet pas parallèles et ne se croisent pas, comme le montre l’image.