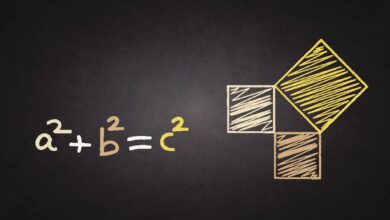Contents
Le mot géométrie vient du grec geos (qui signifie Terre) et metron (qui signifie mesure). La géométrie était extrêmement importante pour les sociétés anciennes, et elle était utilisée pour l’arpentage, l’astronomie, la navigation et la construction. La géométrie telle que nous la connaissons est en fait la géométrie euclidienne, qui a été écrite il y a bien plus de 2 000 ans dans la Grèce antique par Euclide, Pythagore, Thalès, Platon et Aristote, pour n’en citer que quelques-uns. Le texte de géométrie le plus fascinant et le plus précis a été écrit par Euclide, appelé « Éléments ». Le texte d’Euclide est utilisé depuis plus de 2 000 ans.
La géométrie est l’étude des angles et des triangles, du périmètre, de la surface et du volume. Elle diffère de l’algèbre dans la mesure où l’on développe une structure logique où les relations mathématiques sont prouvées et appliquées. Commencez par apprendre les termes de base associés à la géométrie.
Termes de géométrie
Point
Les points indiquent la position. Un point est indiqué par une lettre majuscule. Dans cet exemple, A, B et C sont tous des points. Remarquez que les points sont sur la ligne.
Nommer une ligne
Une ligne est infinie et droite. Si vous regardez l’image ci-dessus, AB est une ligne, AC est également une ligne et BC est une ligne. Une ligne est identifiée lorsque vous nommez deux points sur la ligne et que vous tracez une ligne sur les lettres. Une ligne est un ensemble de points continus qui s’étendent indéfiniment dans l’une ou l’autre de ses directions. Les lignes sont également nommées avec des lettres minuscules ou une seule lettre minuscule. Par exemple, l’une des lignes ci-dessus pourrait être nommée simplement en indiquant un e.
Définitions importantes de la géométrie
Segment de ligne
Un segment de ligne est un segment de ligne droite qui fait partie de la ligne droite entre deux points. Pour identifier un segment de droite, on peut écrire AB. Les points de chaque côté du segment de ligne sont appelés les points d’extrémité.
Ray
Un rayon est la partie de la ligne qui se compose du point donné et de l’ensemble de tous les points d’un côté du point final.
Dans l’image, A est le point final et ce rayon signifie que tous les points partant de A sont inclus dans le rayon.
Angles
Un angle peut être défini comme deux rayons ou deux segments de ligne ayant un point final commun. Le point d’extrémité devient connu sous le nom de sommet. Un angle se produit lorsque deux rayons se rencontrent ou s’unissent au même point d’extrémité.
Les angles représentés sur l’image peuvent être identifiés comme étant l’angle ABC ou l’angle CBA. Vous pouvez également écrire cet angle comme angle B qui nomme le sommet. (point d’extrémité commun aux deux rayons).
Le sommet (dans ce cas B) est toujours écrit comme la lettre du milieu. L’endroit où vous placez la lettre ou le chiffre de votre sommet n’a pas d’importance. Il est acceptable de le placer à l’intérieur ou à l’extérieur de votre angle.
Lorsque vous vous référez à votre manuel scolaire et que vous faites vos devoirs, veillez à être cohérent. Si les angles auxquels vous vous référez dans vos devoirs utilisent des chiffres, utilisez des chiffres dans vos réponses. Quelle que soit la convention d’appellation utilisée dans votre texte, c’est celle que vous devez utiliser.
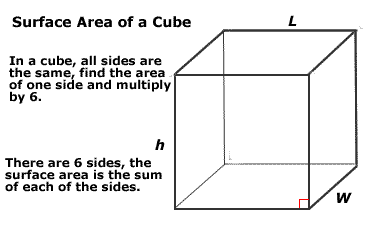
Avion
Un avion est souvent représenté par un tableau noir, un tableau d’affichage, le côté d’une boîte ou le dessus d’une table. Ces surfaces planes sont utilisées pour relier deux ou plusieurs points sur une ligne droite. Un plan est une surface plane.
Vous êtes maintenant prêt à passer aux types d’angles.
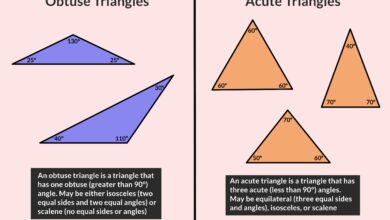
Angles aigus
Un angle est défini comme étant l’endroit où deux rayons ou deux segments de ligne se rejoignent en un point commun appelé le sommet. Voir la partie 1 pour plus d’informations.
Angle aigu
Un angle aigu mesure moins de 90 degrés et peut ressembler aux angles entre les rayons gris de l’image.
Angles droits
Un angle droit mesure exactement 90 degrés et ressemblera à l’angle de l’image. Un angle droit est égal à un quart de cercle.
Angles obtus
Un angle obtus mesure plus de 90 degrés, mais moins de 180 degrés, et ressemblera à l’exemple de l’image.
Angles droits
Un angle droit forme une ligne parfaite.
Un angle droit est de 180 degrés et apparaît comme un segment de ligne.
Angles de réflexes
Un angle de réflexion est supérieur à 180 degrés, mais inférieur à 360 degrés, et ressemblera à l’image ci-dessus.
Angles complémentaires
Deux angles s’additionnant jusqu’à 90 degrés sont appelés angles complémentaires.
Dans l’image présentée, les angles ABD et DBC sont complémentaires.
Angles supplémentaires
Deux angles s’additionnant jusqu’à 180 degrés sont appelés angles supplémentaires.
Dans l’image, l’angle ABD + l’angle DBC sont supplémentaires.
Si vous connaissez l’angle ABD, vous pouvez facilement déterminer ce que l’angle DBC mesure en soustrayant l’angle ABD de 180 degrés.
Postulats fondamentaux et importants
Euclide d’Alexandrie a écrit 13 livres intitulés « Les éléments » vers 300 avant JC. J.-C. Ces livres ont jeté les bases de la géométrie. Certains des postulats ci-dessous ont en fait été posés par Euclide dans ses 13 livres. Ils ont été supposés comme des axiomes mais sans preuve. Les postulats d’Euclide ont été légèrement corrigés au fil du temps. Certains sont énumérés ici et continuent à faire partie de la géométrie euclidienne. Connaissez ces choses. Apprenez-le, mémorisez-le et gardez cette page comme référence pratique si vous pensez comprendre la géométrie.
Il existe des faits, des informations et des postulats de base qu’il est très important de connaître en géométrie. Tout n’est pas prouvé en géométrie, c’est pourquoi nous utilisons certains postulats, qui sont des hypothèses de base ou des déclarations générales non prouvées que nous acceptons. Voici quelques unes des bases et des postulats qui sont destinés à la géométrie d’entrée de gamme. Il y a beaucoup plus de postulats que ceux qui sont énoncés ici. Les postulats suivants sont destinés à la géométrie pour débutants.
Segments uniques
Vous ne pouvez tracer qu’une seule ligne entre deux points. Vous ne pourrez pas tracer une deuxième ligne entre les points A et B.
Cercles
Il y a 360 degrés autour d’un cercle.
Intersection de lignes
Deux lignes peuvent se croiser en un seul point. Dans la figure présentée, S est la seule intersection de AB et CD.
Point médian
Un segment de ligne n’a qu’un seul point médian. Dans la figure présentée, M est le seul point médian de AB.
Bisecteur
Un angle ne peut avoir qu’une seule bissectrice. Une bissectrice est un rayon qui se trouve à l’intérieur d’un angle et qui forme deux angles égaux avec les côtés de cet angle. Le rayon AD est la bissectrice de l’angle A.
Conservation de la forme
Le postulat de la conservation de la forme s’applique à toute forme géométrique qui peut être déplacée sans changer de forme.
Idées importantes
1. Un segment de ligne sera toujours la plus courte distance entre deux points d’un plan. La ligne courbe et les segments de ligne brisée sont une distance plus éloignée entre A et B.
2. Si deux points se trouvent dans un avion, la ligne contenant ces points se trouve dans l’avion.
3. Lorsque deux plans se croisent, leur intersection est une ligne.
4. Toutes les lignes et tous les plans sont des ensembles de points.
5. Chaque ligne a un système de coordonnées (le postulat de la règle).
Sections de base
La taille d’un angle dépend de l’ouverture entre les deux côtés de l’angle et est mesurée en unités appelées degrés, qui sont indiquées par le symbole °. Pour se souvenir de la taille approximative des angles, il faut se rappeler qu’un cercle une fois autour mesure 360 degrés. Pour se souvenir des approximations d’angles, il sera utile de se souvenir de l’image ci-dessus.
Imaginez qu’une tarte entière soit à 360 degrés. Si vous mangez un quart (un quart) de la tarte, la mesure serait de 90 degrés. Et si vous mangiez la moitié de la tarte ? Comme indiqué ci-dessus, 180 degrés est la moitié, ou vous pouvez ajouter 90 degrés et 90 degrés – les deux morceaux que vous avez mangés.
Le rapporteur
Si vous coupez toute la tarte en huit morceaux égaux, quel angle ferait un morceau de la tarte ? Pour répondre à cette question, divisez 360 degrés par huit (le total divisé par le nombre de morceaux). Cela vous indiquera que chaque morceau de la tarte a une mesure de 45 degrés.
En général, pour mesurer un angle, vous utiliserez un rapporteur. Chaque unité de mesure sur un rapporteur est un degré.
La taille de l’angle ne dépend pas de la longueur des côtés de l’angle.
Mesurer les angles
Les angles indiqués sont d’environ 10 degrés, 50 degrés et 150 degrés.
Réponses
1 = environ 150 degrés
2 = environ 50 degrés
3 = environ 10 degrés
Congruence
Les angles congruents sont des angles qui ont le même nombre de degrés. Par exemple, deux segments de ligne sont congruents s’ils sont de même longueur. Si deux angles ont la même mesure, ils sont également considérés comme congruents. Symboliquement, cela peut être montré comme indiqué dans l’image ci-dessus. Le segment AB est congruent avec le segment OP.
Bisecteurs
Les bissectrices font référence à la ligne, au rayon ou au segment de ligne qui passe par le point médian. La bissectrice divise un segment en deux segments congruents, comme démontré ci-dessus.
Un rayon qui se trouve à l’intérieur d’un angle et qui divise l’angle original en deux angles congruents est la bissectrice de cet angle.
Transversal
Une transversale est une ligne qui croise deux lignes parallèles. Dans la figure ci-dessus, A et B sont des lignes parallèles. Notez ce qui suit lorsqu’une transversale coupe deux lignes parallèles :
- Les quatre angles aigus seront égaux.
- Les quatre angles obtus seront également égaux.
- Chaque angle aigu est complémentaire à chaque angle obtus.
Théorème important n°1
La somme des mesures des triangles est toujours égale à 180 degrés. Vous pouvez le prouver en utilisant votre rapporteur pour mesurer les trois angles, puis additionner les trois angles. Voir le triangle montré pour voir que 90 degrés + 45 degrés + 45 degrés = 180 degrés.
Théorème important n°2
La mesure de l’angle extérieur sera toujours égale à la somme de la mesure des deux angles intérieurs éloignés. Les angles éloignés de la figure sont l’angle B et l’angle C. Par conséquent, la mesure de l’angle RAB sera égale à la somme de l’angle B et de l’angle C. Si vous connaissez les mesures de l’angle B et de l’angle C, vous savez automatiquement ce qu’est l’angle RAB.
Théorème important n°3
Si une transversale coupe deux lignes de telle sorte que les angles correspondants sont congruents, alors les lignes sont parallèles. De même, si deux lignes sont coupées par une transversale de telle sorte que les angles intérieurs du même côté de la transversale sont complémentaires, alors les lignes sont parallèles.
Sous la direction de Anne Marie Helmenstine, Ph.D.