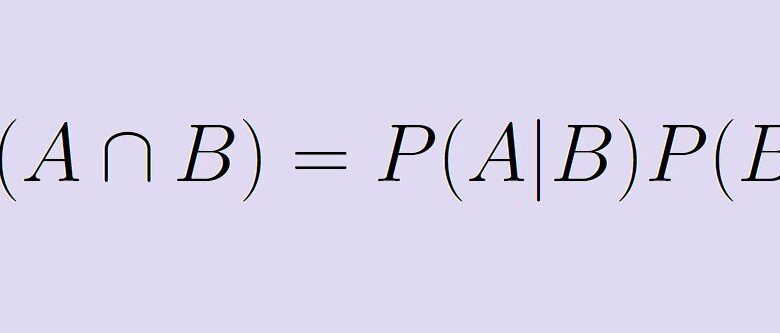
Contents
La probabilité conditionnelle d’un événement est la probabilité qu’un événement A se produise étant donné qu’un autre événement B s’est déjà produit. Ce type de probabilité est calculé en limitant l’espace de l’échantillon sur lequel nous travaillons à l’ensemble B uniquement.
La formule de la probabilité conditionnelle peut être réécrite en utilisant un peu d’algèbre de base. Au lieu de la formule :
P(A | B) = P(A ∩ B) /P( B ),
on multiplie les deux côtés par P( B ) et on obtient la formule équivalente :
P(A | B) x P( B) = P(A ∩ B).
Nous pouvons ensuite utiliser cette formule pour trouver la probabilité que deux événements se produisent en utilisant la probabilité conditionnelle.
Utilisation de la formule
Cette version de la formule est plus utile lorsque nous connaissons la probabilité conditionnelle de A donné B ainsi que la probabilité de l’événement B. Si c’est le cas, nous pouvons alors calculer la probabilité de l’intersection de A donné B en multipliant simplement deux autres probabilités. La probabilité de l’intersection de deux événements est un nombre important car il s’agit de la probabilité que les deux événements se produisent.
Exemples
Pour notre premier exemple, supposons que nous connaissions les valeurs suivantes pour les probabilités : P(A | B) = 0,8 et P( B ) = 0,5. La probabilité P(A ∩ B) = 0,8 x 0,5 = 0,4.
Bien que l’exemple ci-dessus montre comment fonctionne la formule, il n’est peut-être pas le plus éclairant quant à l’utilité de la formule ci-dessus. Nous allons donc examiner un autre exemple. Un lycée compte 400 élèves, dont 120 sont des hommes et 280 des femmes. Parmi les hommes, 60 % sont actuellement inscrits à un cours de mathématiques. Parmi les femmes, 80 % sont actuellement inscrites à un cours de mathématiques. Quelle est la probabilité qu’un étudiant choisi au hasard soit une femme inscrite à un cours de mathématiques ?
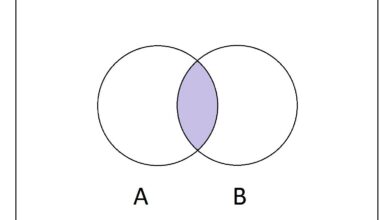
Ici, nous laissons F l’événement « L’étudiant sélectionné est une femme » et M l’événement « L’étudiant sélectionné est inscrit dans un cours de mathématiques ». Nous devons déterminer la probabilité de l’intersection de ces deux événements, ou P(M ∩ F).
La formule ci-dessus nous montre que P(M ∩ F) = P( M|F ) x P( F ). La probabilité qu’une femme soit sélectionnée est P( F ) = 280/400 = 70%. La probabilité conditionnelle que l’étudiant sélectionné soit inscrit à un cours de mathématiques, étant donné qu’une femme a été sélectionnée, est P( M|F ) = 80%. En multipliant ces probabilités, on obtient une probabilité de 80 % x 70 % = 56 % de sélectionner une étudiante inscrite à un cours de mathématiques.
Test d’indépendance
La formule ci-dessus, qui met en relation la probabilité conditionnelle et la probabilité d’intersection, nous permet de savoir facilement si nous avons affaire à deux événements indépendants. Puisque les événements A et B sont indépendants si P(A | B) = P( A ), il découle de la formule ci-dessus que les événements A et B sont indépendants si et seulement si :
P( A ) x P( B ) = P(A ∩ B)
Donc, si nous savons que P( A ) = 0,5, P( B ) = 0,6 et P(A ∩ B) = 0,2, sans rien savoir d’autre, nous pouvons déterminer que ces événements ne sont pas indépendants. Nous le savons parce que P( A ) x P( B ) = 0,5 x 0,6 = 0,3. Ce n’est pas la probabilité de l’intersection de A et B.